基本概念
机器学习中的规则:若......,则......
- 回归:$\text{if }\hat{h}(x)=\hat{y}\text{ then }y=\hat{y}$
- 分类:$\text{if }h(x)>0\text{ , then class = 1 ; else , class = -1}$
- 聚类:$\text{if }\forall j\ne i\text{ , }dist(x,c_i)\le dist(x,c_j)\text{ , then }C(x)=c_i$
逻辑规则:
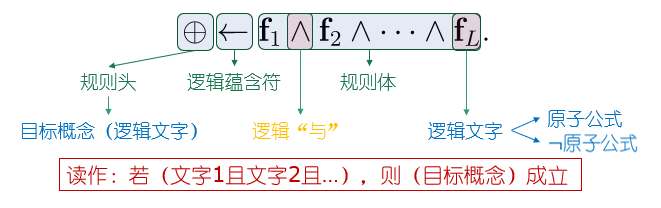
规则集:由规则组成的集合
- 充分性与必要性
- 冲突消解:顺序规则、缺省规则、元规则
命题逻辑 $\to$ 命题规则
- 原子命题: $A,B,C\dots$
- 逻辑连词: $\gets,\to,\leftrightarrow,\lor,\land,\dots$
- 逻辑量词: $\forall,\exist$
一阶逻辑 $\to$ 一阶规则
- 常量: $a,b,c,\dots,1,2,3,\dots$
- 变量: $A,B,C,\dots$
- (n元)谓词/函数: $p/n,f/n,\dots$
- 项:$\text{const }\vert \text{ var }\vert \text{ func/pred }(\text{term}_1,\text{term}_2,\dots)$
- 原子公式:$\text{ func/pred }(\text{term}_1,\text{term}_2,\dots)$
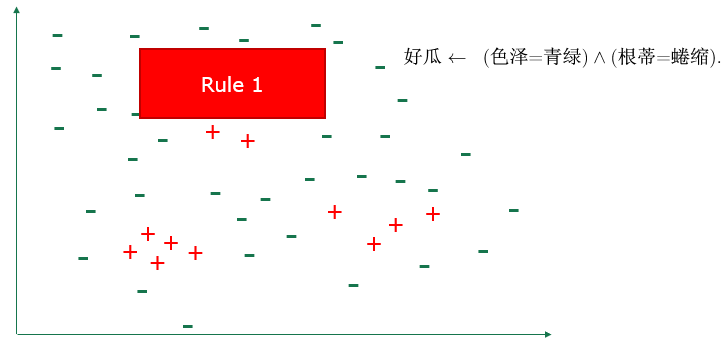
序贯覆盖
在训练集上每学到一条规则,就将规则覆盖的样例去除,然后以剩下的样例组成训练集重复上述的过程(分治策略)
单条规则学习
目标:寻找一组最优的逻辑文字来构成规则体
本质:搜索问题,搜索空间大,容易造成祝贺爆炸
方法:
- 自顶向下:一般到特殊(特化)
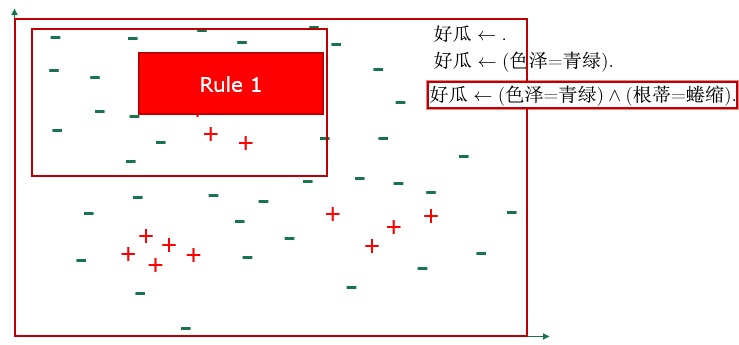
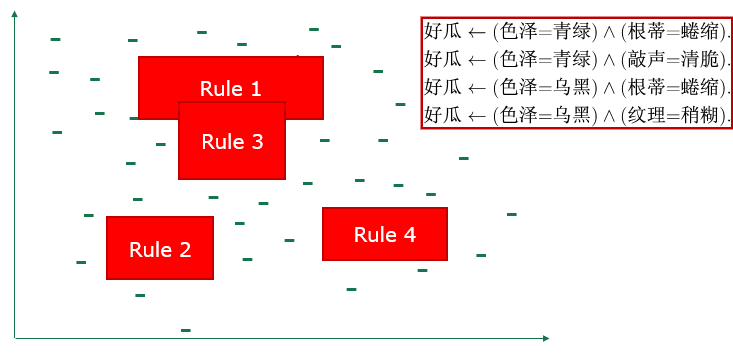
- 自底向上:特殊到一般(泛化)
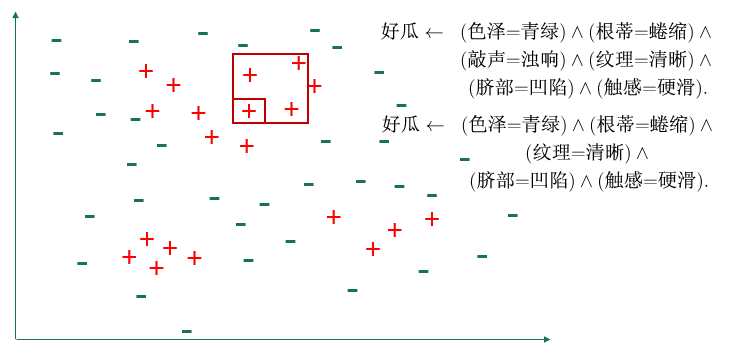
规则评判:增加/删除哪一个候选文字,根据准确率、信息增益、基尼指数等
规避局部最优:集束搜索,每次保留最优的多个候选规则
剪枝优化
序贯覆盖:贪心算法无法得到最优解,需要使用剪枝优化
- 预剪枝:似然率统计量
-
后剪枝:减错剪枝(REP),穷举所有可能的剪枝操作,复杂度比较高,验证集剪枝到准确率无法提高
-
二者结合:
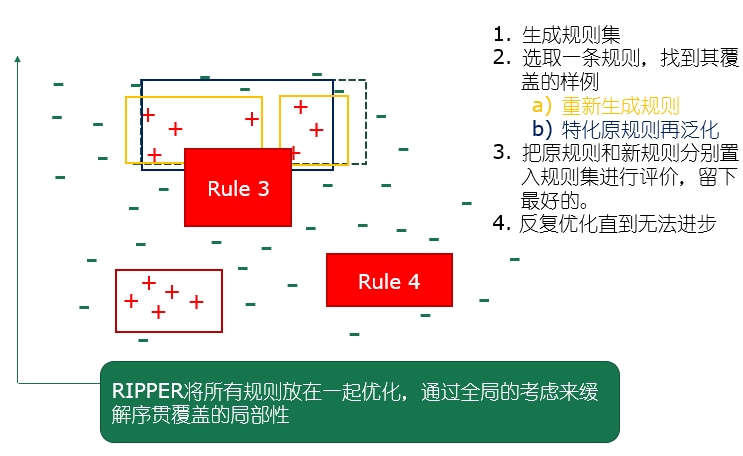
- IREP:每生成一条新规则就对其进行 REP 剪枝
- RIPPER
一阶规则学习
“一阶”的目的:描述一类物体的性质、相互关系

FOIL:序贯覆盖生成规则集,自定向下学习单条规则,然后后剪枝优化规则集
- 候选文字时需要考虑所有可能的选项
- 规则生长的评判标准为 FOIL 增益
归纳逻辑程序设计
目标:完备地学习一阶规则(Horn子句)
仍然采用 序贯覆盖 方法学习规则集,一般采用自底向上策略学习单条规则
- 不需要列举所有可能的候选规则
- 对目标概念的搜索维持在样例附近的局部区域
- 自顶向下策略的搜索空间对规则长度呈指数级增长
最小一般泛化(LGG)
- 泛化:将覆盖率低的规则变换为覆盖率高的规则
- 一般:覆盖率尽可能高
- 最小:变换时对原规则的改动尽可能小
寻找两条规则 LGG 的步骤:
- 找出两条规则中涉及相同谓词的文字
- 考察谓词后括号里的项:
- $LGG(t,t)=t$
- $LGG(s,t),s\ne t$
- s,t不是谓词相同的项,则 $LGG(s,t)=V$ ,V 为任意未出现过的变量
- s,t为谓词相同的项,递归考察其括号内的项
- 删除没有相同谓词出现的文字

逆归结
演绎(deduction)和归纳(induction)
举例来说吧,我开始时曾说你哥哥的行为很不谨慎。请看这只表,不仅下面边缘上有凹痕两处,整个表的上面还有无数的伤痕,这是因为惯于把表放在有钱币、钥匙一类硬东西的衣袋里的缘故。对一只价值五十多镑的表这样不经心,说他生活不检点,总不算是过分吧!
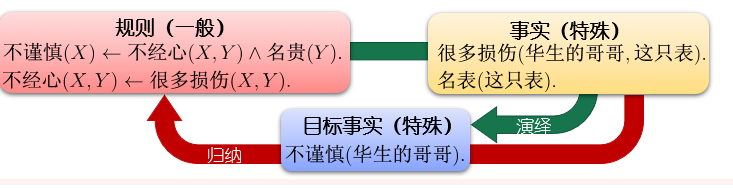
演绎:归结原理,验证逻辑表达式的可满足性
- 输入 $C_1=A\lor L,C_2=B\lor \lnot L$
- 输出 $C=A\lor B$
- 归结项 $C=(C_1-{L})\lor(C_2-{\lnot L})$
归纳:逆归结
- 输入 $C_1=A\lor L,C=A\lor B$
- 输出 $C_2=(C-(C_1-{L}))\lor{\lnot L}$
- 归结商 $C_2=C/C_1$
一阶逆归结
- 置换:用项替换
- 合一:通过置换让两个表达式相等