强化学习基本问题设置

例子：瓜农种瓜

多步决策过程
过程中包含 状态、动作、反馈（奖赏） 等
需要多次种瓜，在过程中不断摸索，才能总结出较好的种瓜策略

抽象化该过程：强化学习（reinforcement learning）

强化学习常用 马尔可夫决策过程 （Markov decision process，MPD）描述

机器所处的环境 E

例如在种西瓜任务中，环境 E 是西瓜生长的自然世界
状态空间 X ： $x\in X$ 是机器感知到的环境的描述

瓜苗长势的描述
机器所能采取的行为空间 A

浇水、施肥等行为
策略（policy）： $\pi:X\rightarrow A$

根据瓜苗状态是缺水时，返回动作浇水
潜在的状态转移（概率）函数： $P:X\times A\times A\rightarrow\mathbb{R}$

瓜苗当前状态缺水，选择动作浇水，有一定概率恢复健康，也有一定概率无法恢复
潜在的奖赏（reward）函数： $R:X\times A\times X\rightarrow\mathbb{R}$

瓜苗健康对应奖赏+1，瓜苗凋零对应奖赏-10

强化学习可以表示为四元组： $E=<X,A,P,R>$

强化学习的目标：机器通过环境 E 中不断尝试，从而学到一个策略 $\pi$ ，使得长期执行该策略后得到的奖励奖赏最大

\[T\text{步积累奖赏: }\mathbb{E}[\frac{1}{T}\sum_{t=1}^T r_t]\\ \gamma\text{折扣积累奖赏: }\mathbb{E}[\sum_{t=0}^{+\infty}\gamma^t r_{t+1}]\\ a=\pi(x)\\ <x_0,a_0,r_1,x_1,a_1,r_2,\dots,x_{T-1},a_{T-1},r_T,x_T>\\ \max \mathbb{E}[\frac{1}{T}\sum_{t=1}^T r_t]\]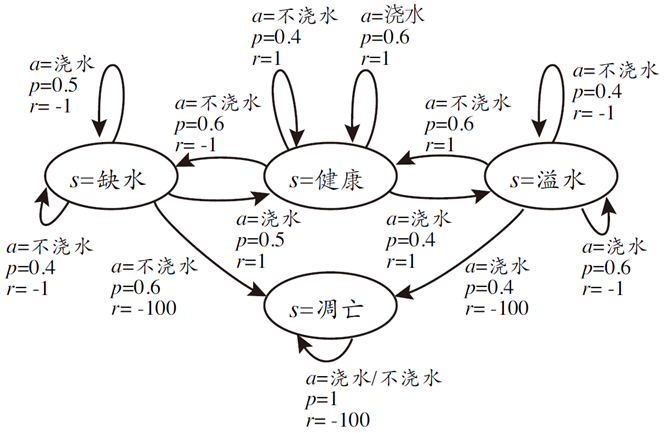

强化学习和监督学习：

监督学习：给定标记样本
强化学习：没有标记样本，通过执行动作之后反馈的奖赏来学习

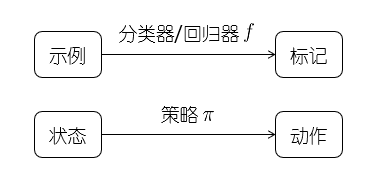
强化学习在某种意义上可以认为是具有“延迟标记信息”的监督学习

K-摇臂赌博机

K-摇臂赌博机（K-Armed Bandit）

只有一个状态，K 个动作
每个摇臂的奖赏服从某个期望未知的分布
执行有限次数动作
最大化积累奖赏

强化学习面临的主要困难：探索-利用窘境（exploration-exploitation dilemma）

仅探索：估计不同摇臂的优劣（奖赏期望的大小）
仅利用：选择当前最优的摇臂

在探索和利用之间进行折中：

ε-贪心
Softmax

ε-贪心

以 $\varepsilon$ 的概率探索，均匀随机选择一个摇臂
以 $1-\varepsilon$ 的概率利用，选择当前平均奖赏最高的摇臂

Softmax

基于当前已知的摇臂平均奖赏来对探索和利用折中

若某个摇臂当前的平均奖赏越大，则它被选择的概率越高
概率分配使用 Boltzmann 分布：

\[P(k)=\frac{\exp(\frac{Q(k)}{\tau})}{\sum_{i=1}^K\exp(\frac{Q(i)}{\tau})}\]

其中 $Q(i)$ 记录当前摇臂的平均奖赏

两种算法都有一个折中参数 $(\varepsilon,\tau)$ ，算法性能取决于具体应用问题

有模型学习

有模型学习（model-based learning）： $E=<X,A,P,R>$

X，A，P，R 均已知
假设状态空间和动作空间均有限

强化学习的目标：找到使积累奖赏最大的策略 $\pi$

策略评估

策略评估：使用某种策略所带来的累计奖赏

状态值函数：从状态 x 出发，使用策略 $pi$ 所带来的积累奖赏

\[\left\{ \begin{aligned} &V_T^\pi(x)=\mathbb{E}_\pi[\frac{1}{T} \sum_{t=1}^T r_t\vert x_0=x]\text{ , T 步积累奖赏}\\ &V_\gamma^\pi(x)=\mathbb{E}_\pi[ \sum_{t=0}^{+\infty} \gamma^t r_{t+1}\vert x_0=x]\text{ , γ 折扣积累奖赏}\\ \end{aligned} \right.\]

状态-动作值函数：从状态 x 出发，执行动作 a 后再使用策略 $\pi$ 所带来的积累奖赏

\[\left\{ \begin{aligned} &Q_T^\pi(x,a)=\mathbb{E}_\pi[\frac{1}{T} \sum_{t=1}^T r_t\vert x_0=x,a_0=a]\\ &Q_\gamma^\pi(x,a)=\mathbb{E}_\pi[ \sum_{t=0}^{+\infty} \gamma^t r_{t+1}\vert x_0=x,a_0=a] \end{aligned} \right.\]

给定 $\pi$ ，值函数的计算：值函数具有简单的递归形式

Bellman 等式：起始点的值等于当前点期望值和下一个点的值之和

T 步积累奖赏：

\[\begin{aligned} V_T^\pi(x)&=\mathbb{E}_\pi[\frac{1}{T} \sum_{t=1}^T r_t\vert x_0=x]\\ &=\mathbb{E}_\pi[\frac{1}{T}r_1 + \frac{T-1}{T}\frac{1}{T-1}\sum_{t=2}^T r_t\vert x_0=x]\\ &=\sum_{a\in A}\pi(x,a)\sum_{x{'}\in X}P^{a}_{x\to x{'}} (\frac{1}{T}R^{a}_{x\to x{'}}+\frac{T-1}{T}\mathbb{E}_\pi[\frac{1}{T-1}\sum_{t=1}^{T-1}r_t\vert x_0=x{'}]) \text{ （全概率公式）}\\ &=\sum_{a\in A}\pi(x,a)\sum_{x{'}\in X}P_{x\in x{'}}^a (\frac{1}{T}R_{x\to x{'}}^a+\frac{T-1}{T}V_{T-1}^{\pi}(x{'})) \end{aligned}\]

$\gamma$ 折扣累积奖赏

\[V_\gamma^\pi(x)=\sum_{a\in A}\pi(x,a)\sum_{x'\in X} P_{x\to x'}^a(R_{x\to x'}^a+\gamma V_\gamma^\pi(x'))\]

给定 $\pi$ ，状态-动作值函数的计算：通过值函数来表示

\[\left\{ \begin{aligned} &Q_T^\pi(x,a)=\sum_{x'\in X}P_{x\to x'}^a (\frac{1}{T}R_{x\to x'}^a+\frac{T-1}{T}V_{T-1}^\pi(x'))\\ &Q_\gamma^\pi(x,a)=\sum_{x'\in X}P_{x\to x'}^a (R_{x\to x'}^a+\gamma V_\gamma^\pi(x')) \end{aligned} \right.\]

最优策略、最优值函数、最优状态-动作值函数

最优策略：最大化累积奖赏

\[\pi^*=\mathop{\arg\max}\limits_\pi \sum\limits_{x\in X}V^\pi(x)\]

最优值函数：

\[\forall x\in X\text{ : }V^*(x)=V^{\pi ^*}(x)\]

最优状态-动作值函数

策略改进

最优策略改进：将非最优策略改进为最优策略

最优值函数/最优策略满足

\[\left\{ \begin{aligned} &V_T^{*}(x)=\mathop{max}_{a\in A}\sum_{x'\in X} P(x\to x')^a(\frac{1}{T}R_{x\to x'}^a +\frac{T-1}{T}V_{T-1}^{*}(x'))\\ &V_\gamma^{*}(x)=\mathop{max}_{a\in A}\sum_{x'\in X} P(x\to x')^a(R_{x\to x'}^a+\gamma V_{\gamma}^{*}(x')) \end{aligned} \right.\\ \downarrow\\ V^{*}(x)=\mathop{max}\limits_{a\in A}Q^{\pi^{*}}(x,a)\]

非最优策略的改进方式：将策略选择的动作改为当前最优的动作

\[\pi '(x)=\mathop{\arg\max}\limits_{a\in A}Q^\pi(x,a)\]

策略迭代

策略迭代（policy iteration）：求解最优策略的方法

随机策略作为初始策略
策略评估+策略改进+策略评估+策略改进+……
直到策略收敛

策略迭代算法的缺点：每次改进策略后都重新评估策略，导致耗时

有模型学习小结

强化学习任务可归结为基于动态规划的寻优问题
与监督学习不同，这里并未涉及到泛化能力，而是为每一个状态找到好的动作

免模型学习

免模型学习（model-free learning）：更加符合实际情况

转移概率、奖赏函数未知
环境中的状态数目未知
假定状态空间有限

免模型学习所面临的困难

策略无法评估
无法通过值函数计算状态-动作值函数
机器只能从一个起始状态开始探索环境

解决困难的办法

多次采样
直接估计每一对状态-动作的值函数
在探索过程中逐渐发现各个状态

蒙特卡罗强化学习

蒙特卡罗强化学习：采样轨迹，用样本均值近似期望

策略评估：蒙特卡罗法
- 从某状态出发，执行某策略
- 对轨迹中出现的每对状态-动作，记录其后的奖赏之和
- 采样多条轨迹，每个状态-动作对的累积奖赏取平均值
策略改进：换入当前最优动作

轨迹： $<x_0,a_0,r_1,x_1,a_1,r_2,\dots,x_{T-1},a_{T-1},r_T>$

蒙特卡罗强化学习可能遇到的问题：轨迹的单一性

解决问题的方法：ε-贪心法

同策略：被评估与被改进的是同一个策略

异策略：被评估与被改进的是不同的策略

时序差分学习

蒙特卡罗强化学习的缺点：低效

求平均时以“批处理式”进行
在一个完整的采样轨迹完成后才对状态-动作值函数进行更新

克服缺点的办法：时序差分（temporal difference，TD）学习

时序差分学习：

增量式进行状态-动作值函数更新

\[Q_t^\pi(x,a)=\frac{1}{t}\sum_{i=1}^t r_i\\ \downarrow\\ Q_{t+1}^\pi(x,a)=Q_{t}^\pi(x,a)+\frac{1}{t+1} (r_{t+1}-Q_t^\pi(x,a))\]

ε-贪心法
- 同策略：Sarsa 算法
- 异策略：Q-学习（Q-learning）

值函数近似

问题：前面都是假定状态空间是离散（有限）的，如果状态空间是连续（无限）的，该怎么办？

连续状态空间面临的困难：值函数不再是关于状态的“表格值函数”（tabular value function）

解决困难的办法：值函数近似

假定状态空间 $X=\mathbb{R}^n$
考虑线性近似
假定行为空间有限

值函数近似

将值函数表达为状态的线性函数

\[V_\theta(x)=\theta^T x\\\]

$\theta$ 为状态向量， $x$ 为参数向量

使用最小二乘误差来度量学到的值函数与真实的值函数 $V^\pi$ 之间的近似程度

\[\varepsilon_\theta=\mathbb{E}_{x\thicksim\pi}[(V^\pi(x)-V_\theta(x))^2]\]

用梯度下降法更新参数向量，求解优化问题

状态-动作值函数的线性近似

\[Q_\theta(x,a)=\theta^T(x,a)\\ a=(0,\dots,1,dots,0)\]

非线性值函数近似：核方法

模仿学习

强化学习任务中多步决策的搜索空间巨大，基于积累奖赏来学习很多步之前的合适决策非常困难

缓解方法：直接模仿人类专家的状态-动作对来学习策略

相当于告诉机器在什么状态下应该选择什么动作
引入了监督学习来学习策略

直接模仿学习：

利用专家的决策轨迹，构造数据集 D ：状态作为特征，动作作为标记
利用数据集 D ，使用分类/回归算法即可学的策略
将学得的策略作为初始策略
策略改进，从而获得更好的策略

人类专家决策轨迹数据：

\[\{\tau_1,\tau_2,\dots,\tau_m\}\\ \tau_i=<s_1^i,a_1^i,s_2^i,a_2^i,\dots,s_{n_i+1}^i>\]

构造出的“有标记”数据集：

\[D=\{(s_1,a_1),(s_2,a_2),\dots,(s_{\sum_{i=1}^m n_i},a_{\sum_{i=1}^m n_i})\}\]

强化学习任务中，设计合理的符合应用场景的奖赏函数往往相当困难

缓解方法：从人类专家提供的范例数据中反推出奖赏函数

逆强化学习（inverse reinforcement learning）：寻找某种奖赏函数使得范例数据是最优的，然后使用这个奖赏函数来训练策略

总结

强化学习：多步决策过程
有模型学习：基于动态规划的寻优
如何处理环境中的未知因素：
- 蒙特卡罗强化学习
- 时序差分学习
如何处理连续状态空间：值函数近似
如何提速强化学习过程：
- 直接模仿学习
- 逆强化学习

机器学习——强化学习

强化学习基本问题设置

K-摇臂赌博机

有模型学习

策略评估

策略改进

策略迭代

免模型学习

蒙特卡罗强化学习

时序差分学习

值函数近似

模仿学习

总结

参考资料

CATALOG

FEATURED TAGS