k近邻学习
k近邻(k-nearest neighbor,kNN)学习是一种监督学习方法
- 确定训练样本和距离度量
- 对于某个给定的测试样本,找到训练集中距离最近的k个样本;对于分类问题使用“投票法”获得预测结果,回归问题使用“平均法”。还可以基于距离进行加权平均或加权投票
- 投票法:选择k个样本最多的类别
- 平均法:选择k个样本的实值输出标记的平均值
k近邻学习属于“懒惰学习”
- 懒惰学习(lazy learning):训练阶段仅保存样本,训练时间开销为零,
- 急切学习(eager learning):在训练阶段就对样本进行学习
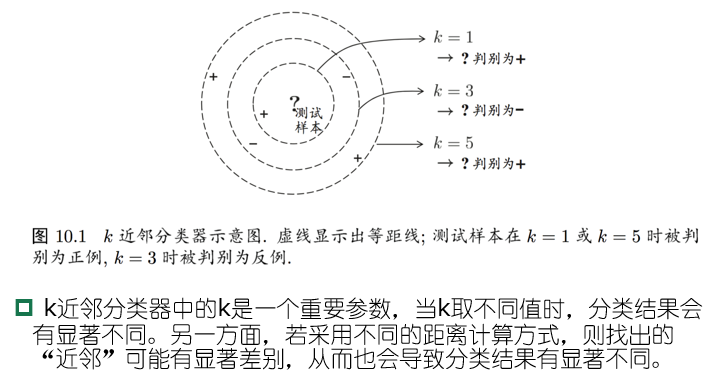
分析1NN二分类错误率 $P(err)$
测试样本 $x$ ,最近邻样本 $z$
\[P(err)=1-\sum\limits_{c\in \mathcal{Y}}P(c\vert x)P(c\vert z)\]假设样本独立同分布,在 $x$ 附近 $\delta$ 距离范围内总能找到一个训练样本
令 $c^*=\mathop{\arg\max}\limits_{c\in\mathcal{Y}}P(c\vert x)$ 表示最优分类器的结果,有
\[\begin{aligned} P(err) &=1-\sum\limits_{c\in mathcal{Y}}P(c\vert x)P(c\vert z)\simeq 1-\sum\limits_{c\in\mathcal{Y}}P^2(c\vert x)\\ &\le 1-P^2(c^*\vert x)\le 2\times(1-P(c^*\vert x)) \end{aligned}\]最近邻分类虽然简单,但是它的泛化错误率不超过贝叶斯最优分类器错误率的两倍
多维缩放
低维嵌入
上述讨论都基于一个重要假设:任意测试样本附近任意小的距离范围内总能找到一个训练样本,即训练样本的采样密度足够大;但实际问题中很难满足
维数灾难:在高维情形下出现的数据样本稀疏、距离计算困难等问题,是所有机器学习方法共同面临的严重障碍
缓解维数灾难的重要途径是降维(dimension reduction)
- 通过数学变换,将原始高维属性空间转变为一个低维”子空间“(subspace),这个空间中样本密度大幅度提升,距离计算也变得容易
为什么能进行降维?
- 数据样本虽然是高维的,但与学习任务密切相关的也许只是某一个低维分布,即高维空间中的一个”低维嵌入“(embedding),因而可以对数据有效降维
多维缩放
多维缩放(multiple dimensional scaling,MDS):要求原始空间中样本之间的距离在低维空间中得以保持
假定有m个样本,在原始空间中的距离矩阵为 $D\in \mathbb{m\times m}$ ,矩阵元素为 $dist_{ij}$
目标是获得样本在 $d’$ 维空间中的欧氏距离等于原始空间的距离,即 $\Vert z_i-z_j\Vert =dist_{ij}$
令 $B=Z^TZ\in\mathbb{m\times m}$ ,其中B为降维后的内积矩阵, $b_ij=z_i^Tz_j$ ,有
\[\begin{aligned} dist_{ij}^2 &=\Vert z_i\Vert^2+\Vert z_j\Vert^2 -2z_i^Tz_j\\ &=b_{ii}+b_{jj}-2b_{ij} \end{aligned}\]为了便于讨论,令降维后的样本Z被中心化,即 $\sum\limits_{i=1}^m z_i=0$ ,显然矩阵B的行列之和均为零,即
\[\sum\limits_{i=1}^m b_ij=\sum\limits_{j=1}^m b_ij=0\]易知
\[\sum\limits_{i=1}^m dist_{ij}^2=tr(B)+mb_{jj}\\ \sum\limits_{j=1}^m dist_{ij}^2=tr(B)+mb_{ii}\\ \sum\limits_{i=1}^m\sum\limits_{j=1}^m dist_{ij}^2=2m\:tr(B)\]其中 $tr(B)=\sum\limits_{i=1}^m\Vert z_i\Vert^2$ ,令
\[\sum\limits_{i=1}^m dist_{i\cdot}^2=tr(B)+mb_{ij}\\ \sum\limits_{j=1}^m dist_{\cdot j}^2=tr(B)+mb_{ij}\\ \sum\limits_{i=1}^m\sum\limits_{j=1}^m dist_{\cdot\cdot}^2=\frac{1}{m^2}\]由此即可通过降维前后保持不变的距离矩阵D求取内积矩阵B
\[b_{ij}=-\frac{1}{2}(dist_{ij}^2-dist_{i\cdot}^2-dist_{\cdot j}^2+dist_{\cdot\cdot}^2)\]对矩阵B做特征值分解(eigenvalue decomposition)
\[B=V\Lambda V^T\]其中 $\Lambda=diag(\lambda_1,\dots,\lambda_d)$ 为特征值构成的对角矩阵,且满足 $\lambda_1\ge\cdots\ge\lambda_n$ ;
假定有 $d^*$ 个非零特征值,
它们构成对角矩阵 $\Lambda_=diag(\lambda_1,\cdots,\lambda_{d^})$ ,其中 $V$ 为特征向量矩阵,
令 $V_$ 表示相应的特征矩阵,则Z可表达为 $Z=\Lambda_^\frac{1}{2}V_^T\in \mathbb{d^\times m}$
在实际应用中为了尽可能有效降维,仅需要降维后的距离与原始空间中的距离尽可能接近,而不必严格相等。此时可取 $d’\ll d$ 个最大特征值构成对角矩阵 $\hat{\Lambda}=diag(\lambda_1,\cdot,\lambda_{d’})$ ,令 $\hat{V}$ 表示相应的特征向量矩阵,则Z可表达为
\[Z=\hat{\Lambda}^{\frac{1}{2}}\hat{V}^T\in\mathbb{R}^{d'\times m}\]
省流: MDS核心是保持降维前后任意两点的距离度量不变。为了得到降维后的Z,先从距离矩阵Dist得到降维后的内积矩阵B,根据B特征分解公式和定义式联立,得到Z。
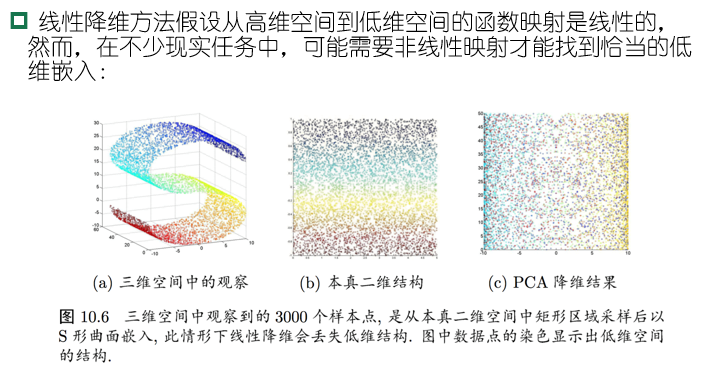
线性降维方法
一般来说,欲获得低维子空间,最简单的是对原始高维空间进行线性变换。给定d维空间中的样本 $X=(x_1,\dots,x_m)\in\mathbb{R}^{d\times m}$ ,变换之后得到 $d’\le d$ 维空间中的样本
\[Z=W^TX\]变换矩阵W可视为 $d’$ 个d维属性向量,对低维子空间性质的不同要求可通过对W施加不同的约束来实现
主成分分析
主成分分析(principal component analysis,PCA)
对于正交属性空间中的样本点,如何使用一个超平面对所有的样本进行恰当的表达?
若存在这样的超平面,应该具有如下性质:
- 最近重构性:样本点到超平面的距离都足够近
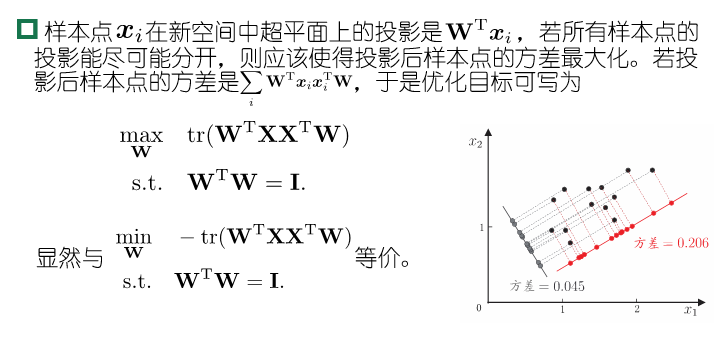
- 最大可分性:样本点在这个超平面上的投影尽可能分开
基于上面两种性质,分别得到PCA的两种等价推导
最近重构性
对样本中心化, $\sum x_i=0$ ,再假定投影变换后得到的新坐标系为 ${w_1,\dots,w_d}$ ,其中 $w_i$ 是标准的正交基向量
\[\Vert w_i\Vert_2=1,w_i^Tw_j=0(i\ne j)\]若丢弃新坐标系中的部分坐标,将维度降低到 $d’<d$ ,则样本在低维坐标系中的投影是 $z_i=(z_{i1};\dots;z_{id’}),z_{ij}=w_j^Tx_i$ 是 $x_i$ 在低维坐标系下第j维的坐标,若基于 $z_i$ 来重构 $x_i$,得到
\[\hat{x}_i=\sum\limits_{j=1}^{d'}z_{ij}w_j\]考虑整个训练集,原样本点 $x_i$ 和基于投影重构的样本点 $\hat{x}_i$ 之间的距离为
\[\begin{aligned} \sum\limits_{i=1}^{m}\Vert \sum\limits_{j=1}^{d'}z_{ij}w_j-x_i\Vert_2^2 &=\sum\limits_{i=1}^m z_i^Tz_i-2\sum\limits_{i=1}^m z_i^TW^Tx_i +const\\ &\propto -tr(W^T(\sum\limits_{i=1}^m x_ix_i^T)W) \end{aligned}\]目标是最小化上式,考虑到 $w_j$ 是标准正交基, $\sum\limits_{i}x_ix_i^T$ 是协方差矩阵,有
\[\min\limits_{W} -tr(W^TXX^TW)\\ s.t.\quad W^TW=I\]是PCA的优化目标
最大可分性
PCA的求解
对优化式使用拉格朗日乘子法可得
\[XX^TW=\lambda W\]只需对协方差矩阵 $XX^T$ 进行特征值分解,并将求得的特征值排序: $\lambda_1\ge\lambda_d$ ,然后取前 $d’$ 个特征值对应的特征向量构成 $W=(w_1,\dots,w_{d’})$ ,得到的W即主成分分析的解

省流:PCA的核心是得到数量少于原始空间维数的正交基(主成分)。为了得到主成分,对样本X中心化,计算协方差矩阵 $XX^T$ ,做特征值分解,对特征值排序。
降维后低维空间的维数 $d’$ 的确定方式:
- 用户指定
- 降维后维数值在不同的低维空间中对k近邻分类器进行交叉验证
- 设置重构阈值
PCA仅需要保留W和样本的均值向量就可以通过简单的向量减法、矩阵-向量乘法将新样本投影到低维空间中
降维虽然会导致信息的损失,但优点在于:
- 使得样本的采样密度增大
- 当数据受到噪声影响时,最小的特征值所对应的特征向量和噪声有关,舍弃可以起到去噪的效果
核化线性降维
核化主成分分析(kernelized PCA,KPCA):非线性降维的一种常用方法,基于核技巧对线性降维方法进行”核化“(kernelized)
假定将在高维特征空间中把数据投影到由W确定的超平面上,即PCA欲求解
\[(\sum\limits_{i=1}^m z_iz_i^T)W=\lambda W\]其中 $z_i$ 是样本点 $x_i$ 在高维特征空间中的像。令 $\alpha_i=\frac{1}{\lambda}z_i^TW$
\[W=\frac{1}{\lambda}(\sum\limits_{i=1}^mz_iz_i^T)W=\sum\limits_{i=1}^m z_i\frac{z_i^TW}{\lambda}=\sum\limits_{i=1}^m z_i\alpha_i\]假定 $z_i$ 是由原始属性空间中的样本点 $x_i$ 通过映射 $\phi$ 产生,即
\[z_i=\phi(x_i)\]若 $\phi$ 能够被显式地表达出来,则通过它将样本映射到高维空间,再在特征空间中实施PCA即可,得到
\[(\sum\limits_{i=1}^m\phi(i=1)^m\phi(x_i)\phi(x_i)^T)W=\lambda W\\ W=\sum\limits_{i=1}^m \phi(x_i)\alpha_i\]一般情形下,引入核函数代替核映射
\[\kappa(x_i,x_j)=\phi(x_i)^T\phi(x_j)\]又由 $W=\sum\limits_{i=1}^m \phi(x_i)\alpha_i$ 带入优化式 $(\sum\limits_{i=1}^m\phi(i=1)^m\phi(x_i)\phi(x_i)^T)W=\lambda W$ ,得到
\[KA=\lambda A\]其中K为 $\kappa$ 的核矩阵, $(K)_{ij}=\kappa(x_i,x_j),A=(\alpha_1;\dots;\alpha_m)$
上式为特征值分解问题,取K最大的 $d’$ 个特征值对应的特征向量得到解
对新样本x,其投影后的第j维坐标为
\[\begin{aligned} z_j=w_j^T\phi(x) &=\sum\limits_{i=1}^m\alpha_i^j\phi(x_i)^T\phi(x)\\ &=\sum\limits_{i=1}^m\alpha_i^j\kappa(x_i,x) \end{aligned}\]其中 $\alpha_i$ 已经经过规范化。由上式可知,为获得投影后的坐标,KPCA需对所有样本求和,计算开销比较大
流形学习
流形学习(manifold learning):借鉴了拓扑流形概念的降维方法
”流形“是在局部与欧氏空间同胚的空间,在局部具有欧氏空间的性质,能用欧氏距离来进行距离计算
若低维流形嵌入到高维空间,则数据样本在高维空间的分布虽然看上去比较复杂,但在局部仍具有欧氏空间的性质,因此,可以容易地在局部建立降维映射关系,然后再设法将局部映射关系推广到全局
当维数降至二维或三维,能对数据可视化展示。流形学习也可用于可视化
等度量映射(Isometric Mapping,Isomap)
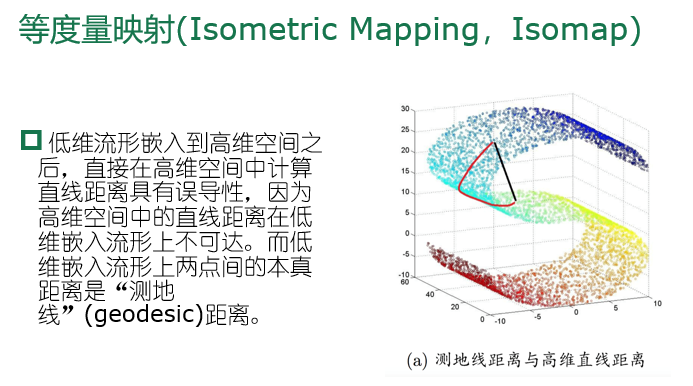


省流:IsoMap的核心是利用最近邻可达构造距离矩阵保持降维后样本相关性,同时解决流形降维的问题。为了得到降维后的Z,设置近邻参数k,样本点和近邻点设置欧氏距离,其他点设为无穷大,构造Dist矩阵,使用MDS算法,得到低维投影。
局部线性嵌入(Locally Linear Embedding,LLE)
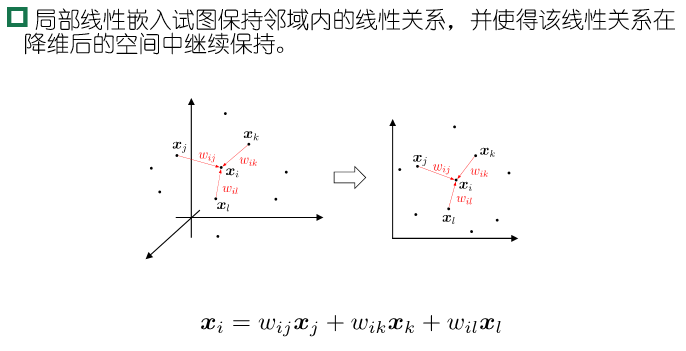
LLE先为每个样本 $x_i$ 找到其近邻下标集合 $Q_i$ ,然后计算出基于 $Q_i$ 中的样本点对 $x_i$ 进行线性重构的系数 $w_i$ :
\[\min\limits_{w_1,\dots,w_m}\sum\limits_{i=1}^m \Vert x_i-\sum\limits_{j\in Q_i}w_{ij}x_j\Vert_2^2\\ s.t.\quad \sum\limits_{j\in Q_j}w_{ij}=1\]其中 $x_i$ 和 $x_j$ 均已知,令 $C_{jk}=(x_i-x_j)^T(x_i-x_k)$ , $w_{ij}$ 有闭式解
\[w_{ij}=\frac{\sum_{k\in Q_i}C^{-1}_{jk}}{\sum_{l,s\in Q_i}C^{-1}_{ls}}\]LLE在低维空间中保持 $w_i$ 不变,于是 $x_i$ 对应的低维空间坐标 $z_i$ 可以通过下式求解:
\[\min\limits_{w_1,\dots,w_m}\sum\limits_{i=1}^m \Vert z_i-\sum\limits_{j\in Q_i}w_{ij}z_j\Vert_2^2\]令 $Z=(z_1,\dots,z_m)\in \mathbb{R}^{d^{‘}\times m},(W){ij}=w{ij}$ ,
\[M=(I-W)^T(I-W)\]最优化式可以重写为下式,并通过特征值分解求解
\[\min\limits_{Z}tr(ZMZ^T)\\ s.t.\quad ZZ^T=I\]
LLE的核心是利用最近邻记录中心样本点的线性构成,保持降维后样本相关性。为了得到降维后的Z,设置近邻参数k,计算线性矩阵W,再计算M,对M特征分解得到低维投影。
度量学习
在机器学习中,对高维数据降维的主要目的是希望找到一个合适的低维空间,在此空间中进行学习能比原始空间性能更好。每个空间对应了在样本属性上定义的一个距离度量,而寻找合适的空间,实质上就是寻找一个合适的距离度量。
为什么不尝试”学习“出一个合适的距离度量?
对距离度量进行学习,必须有一个便于学习的距离度量表达形式,比如平方欧氏距离
\[dist_{ed}^2(x_i,x_j)=\Vert x_i-x_j\Vert_2^2\]引入属性权重w,得到
\[dist_{wed}^2(x_i,x_j)=w_1\cdot dist_{ij,1}^2+\cdots+w_d\cdot dist_{ij,d}^2=(x_i-x_j)^TW(x_i-x_j)\]其中 $W=diag(w)$ 是一个对角矩阵,可以通过学习确定
权重矩阵的非对角元素均为零,说明坐标轴是正交的,即属性之间无关。但实际中存在属性相关,此时坐标轴不再正交,将W替换为普通的半正定矩阵M,得到马氏距离(mahalanobis distance)
\[dist_{mah}^2(x_i,x_j)=(x_i-x_j)^TW(x_i-x_j)=\Vert x_i-x_j\Vert^2_M\]M称为度量矩阵,而度量学习则是对M进行学习。由于为了保持距离非负且对称,M必须是(半)正定对称矩阵,即必须有正交基P使得M能写为 $M=PP^T$
对M进行学习需要设置一个目标,假定我们希望提高近邻分类器的性能,则可将M直接嵌入到近邻分类器的评价指标中去,通过优化该性能指标相应地求得M。
近邻成分分析
近邻成分分析(neighborhood component analysis,NCA):
近邻成分分析判别时使用多数投票法,替换为概率投票法。对任意样本 $x_j$ 对采样 $x_i$ 分类结果影响为:
\[p_{ij}=\frac{exp(-\Vert x_i-x_j\Vert_M^2)}{\sum_{j\ne i} exp(-\Vert x_i-x_j\Vert_M^2)}\]以留一法(LOO)正确率的最大化为目标,则可计算 $x_i$ 的留一法正确率,即它被自身之外的所有样本正确分类的概率
\[p_i=\sum\limits_{j\in \Omega_i}p_{ij}\]其中 $\Omega_i$ 表示与采样样本属于相同类别的样本的下标集合
整个样本上的留一法正确率为
\[\sum_{i=1}^m p_i=\sum\limits_{i=1}^m\sum\limits_{j\in\Omega_i}p_{ij}\]由 $M=PP^T$ ,则NCA的优化目标为
\[\min\limits_{P}1-\sum\limits_{i=1}^m\sum\limits_{j\in\Omega_i}\frac{exp(-\Vert P^Tx_i-P^Tx_j\Vert_2^2)}{\sum_{j\ne j}exp(-\Vert P^Tx_i-P^Tx_j\Vert_2^2)}\]求解即得到最大化近邻分类器LLO正确率的距离度量矩阵M
省流:NCA的核心是求得伪马氏距离矩阵M。基于留一法和KNN,以采样点正确分类概率最大为优化目标,对非凸问题梯度下降求解M。
相关资料
- 矩阵的迹——性质及运算
- PCA 主成分分析(特征值分解、SVD分解)
- 山竹果 BLOG 特征分解
- 机器学习算法总结(十二)——流形学习(Manifold Learning)
- 度量学习(Metric Learning)基础概念介绍——2020.2.2
- 近邻成分分析NCA详解