间隔与支持向量
线性模型:在样本空间中寻找一个超平面,将不同类别的样本分开
超平面方程: $w^T+b=0$
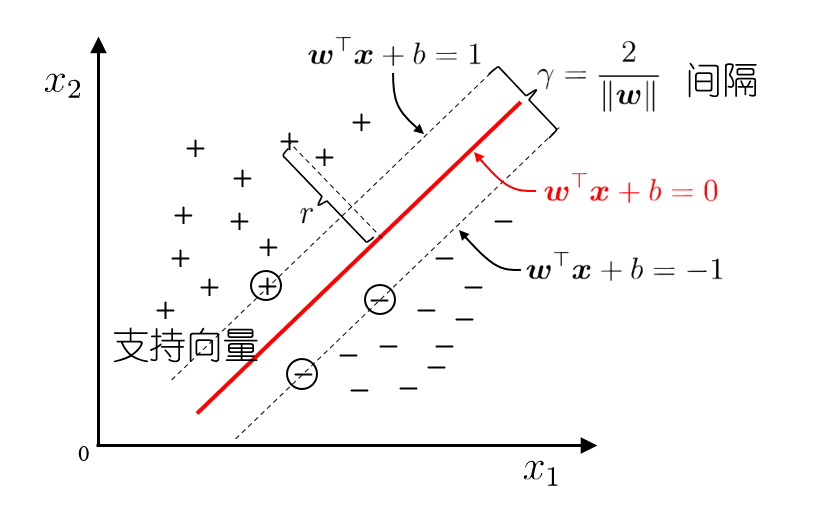
最大间隔:寻找参数 $(w,b)$ ,使得 $\gamma$ 最大
\[\mathop{\arg\max}\limits_{w,b}\frac{2}{\Vert w\Vert} \\ s.t.\quad y_i(w^Tx_i+b)\ge 1,i=1,2,\dots,m \\ \Longrightarrow \\ \mathop{\arg\min}\limits_{w,b}\frac{1}{2}\Vert w\Vert^2 \\ s.t.\quad y_i(w^Tx_i+b)\ge 1,i=1,2,\dots,m\]带约束的优化问题
\[\min\limits_{x\in D}f(x)\\ s.t.\quad g_i(x)\le 0,i=1,2,\dots,q\\ h_j(x)=0,j=q+1,\dots,m\]$f(x),g(x),h(x)$ 分别为目标函数、不等式约束、等式约束
- 若三个函数都是线性函数,则该优化问题为线性规划
- 若任何一个是非线性函数,则该优化问题为非线性规划
- 若目标函数为二次函数,约束全为线性函数,则该优化问题为二次规划
- 若目标函数和不等式约束为凸函数,等式约束为线性函数,则该优化问题为凸优化
凸优化的任意局部极值点也是全局极值点,局部最优也是全局最优
等式约束
考虑一个简单的优化问题
\[\min f(x)=x_1+x_2\\ s.t.\quad h(x)=x_1^2+x_2^2-2=0\]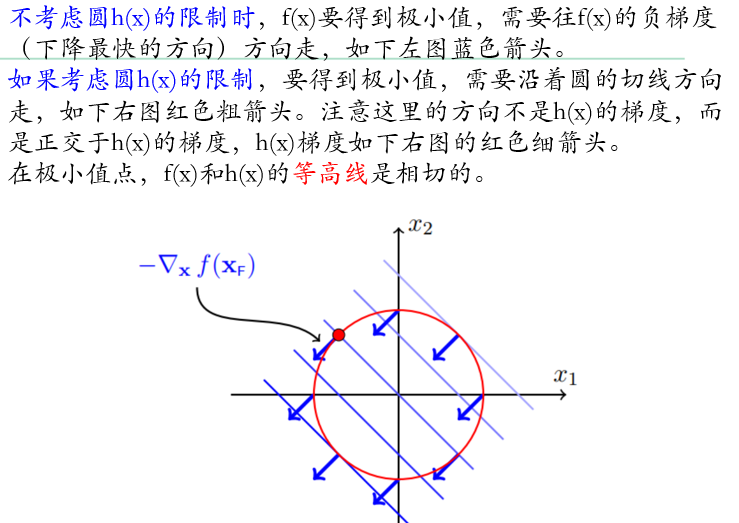
在关键的极小值处,目标函数的负梯度和等式约束的梯度方向相同
\[\nabla f(x^*)=\mu\nabla_x h(x^*)\]所以可以定义拉格朗日乘数法
\[\mathcal{L}(x,\mu)=f(x)+\mu h(x)\\ Then\:x^*\:a\:local\:minimum\Leftrightarrow there\:exists\:a\:unique\:\mu^*s.t.\\ \left\{ \begin{aligned} & \nabla_x \mathcal{L}(x^*,\mu^*)=0 \quad\leftarrow\:encodes\: \nabla f(x^*)=\mu\nabla_x h(x^*)\\ & \nabla_\mu \mathcal{L}(x^*,\mu^*)=0 \quad\leftarrow\:encodes\: h(x^*)=0 \end{aligned} \right.\]特别注意,优化问题是凸优化,上面两个条件求得的解就是极小值点,并且是全局极小值;不是凸优化问题,两个条件只是极小值点的必要条件,需要附加一个正定条件才能变成充要条件,即
\[y^t(\nabla_{xx}^2\mathcal{L}(x^*,\mu^*))y\ge 0 \quad \forall y\:s.t.\:\nabla_{x}h(x^*)^ty=0\\ \leftarrow\:Positive\:definite\:Hessian\:tells\:us \:we\:have\:a\:local\:minimum\]不等式约束
$g(x)\le 0$ 是一个区域,由很多等高线堆叠而成,称为可行域
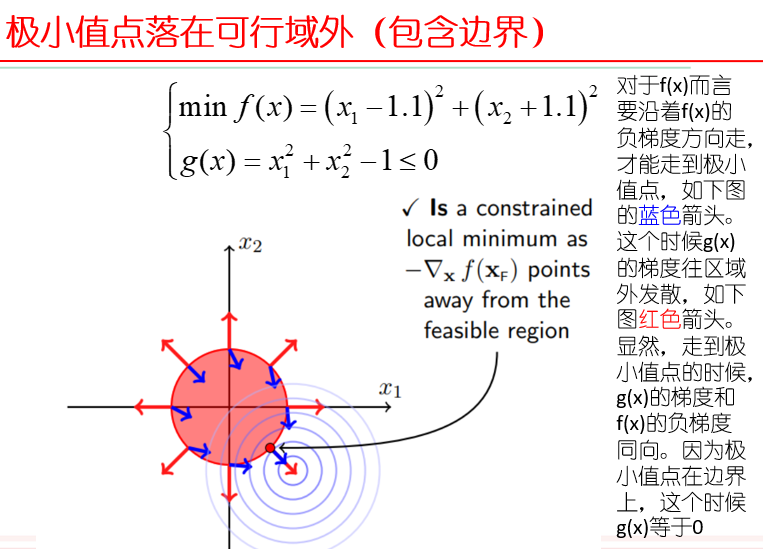
- 极小值点落在可行域内(不包含边界):可行域限制不起作用,相当于没有约束,直接按照目标函数梯度等于0秋季
- 极小值点落在可行域外(包含边界):可行域限制起作用,不等式约束类似于等值约束
因此定义不等式约束的拉格朗日乘数法
\[\mathcal{L}(x,\lambda)=f(x)+\lambda g(x)\\ Then\:x^*\:is\:a\:local\:minimum\:\\ \Leftrightarrow\: there\:exists\:a\:unique\:\lambda^*\:s.t.\\ \left\{ \begin{aligned} & \nabla_x\mathcal{L}(x^*,\lambda^*)=0\\ & \lambda^*\ge 0\\ & \lambda^*g(x^*)=0 \\ & g(x^*)\le 0 \end{aligned} \right.\]上面的三个条件就是著名的KKT条件,整合了极小值点在可行域内、可行域外的两种情况
特别注意:如果优化问题是凸优化,那么KKT条件就是极小值点(而且是全局极小值)存在的充要条件;如果不是凸优化,那么KKT条件只是必要条件
不是凸优化的话,需要附加一个正定条件才能变成充要条件
$\nabla_xx\mathcal{L}(x^,\lambda^)$ 必须是正定的
多个等式和不等式约束
\[\min\limits_{x\in \mathbb{R}^2}f(x)\quad s.t.\\ h_i(x)=0\:for\:i=1,\dots,l\\ \:g_j(x)\le 0\:for\:j=1,\dots,m\]拉格朗日乘数法定义为
\[\mathcal{L}(x,\mu,\lambda)=f(x)+\mu^th(x)+\lambda^tg(x)\\ exists\:a\:unique\:\lambda^*\quad s.t.\\ \left\{ \begin{aligned} & \nabla_x\mathcal(x^*,\mu^*,\lambda^*)=0\\ & \lambda_j\ge 0\quad for\:j=1,\dots,m\\ & g_j(x^*)\le 0\quad for\:j=1,\dots,m\\ & h(x^*)=0\\ & y^t(\nabla_{xx}^2\mathcal{L}(x^*,\mu^*,\lambda^*))y\ge 0 \end{aligned} \right.\]对偶问题
对于转化为拉格朗日乘数形式的最优化问题,如果有m个不等式约束,就要讨论 $2^m$ 种情况
原问题
\[\min\frac{1}{2}\Vert w\Vert^2\quad s.t.\\ 1-y_i(w^Tx_i+b)\le 0\]拉格朗日乘数法
第一步:引入拉格朗日系数 $\alpha_i\ge 0$ 得到拉格朗日函数
\[L(w,b,\alpha)=\frac{1}{2}\Vert w\Vert^2+ \sum\limits_{i=1}^m\alpha_i(1-y_i(w^Tx_i+b))\]第二步:令 $L(w,b,\alpha)$ 对 $(w,b)$ 求偏导为零得到
\[w=\sum\limits_{i=1}^m\alpha_i y_i x_i,\quad 0=\sum\limits_{i=1}^m\alpha_i y_i \\ \rightarrow-\frac{1}{2}w^Tw+\sum\limits_{i=1}^m\alpha_i\]第三步:回代可得
\[\min\limits_{\alpha}-\sum\limits_{i=1}^m\alpha_i +\frac{1}{2}\sum\limits_{i=1}^m\sum\limits_{j=1}^m \alpha_i\alpha_j y_i y_j x_i^T x_j \\ s.t.\quad \sum\limits_{i=1}^m\alpha_i y_i=0, \quad \alpha_i\ge 0\]解的稀疏性
最终模型:
\[f(x)=w^Tx+b=\sum\limits_{i=1}^m\alpha_i y_i x_i^T x+b\]KKT条件:
\[\left\{ \begin{aligned} & \alpha_i\ge 0\\ & y_if(x_i)\ge 1\\ & \alpha_i(y_if(x_i)-1)=0 \end{aligned} \right.\]所以必有 $\alpha_i=0 或 y_if(x_i)=1$
支持向量机解的稀疏性:训练结束后,大部分的训练样本都不需要保留,最终模型仅与支持向量有关
高效求解法-SMO
SMO(sequential minimal optimization)基本思路:不断执行下面两个步骤直至收敛
- 选取一对需要更新的变量 $\alpha_i,\alpha_j$
- 固定 $\alpha_i,\alpha_j$ 以外的参数,求解对偶问题更新这两个参数
用一个变量表示另一个变量,回代入对偶问题可以得到一个单变量的二次回归,该问题具有闭式解
偏移向量b:通过支持向量来确定
核函数
如果不存在能够正确划分两类样本的超平面,将样本从原始空间映射到更高维的特征空间,使得样本在这个特征空间内线性可分
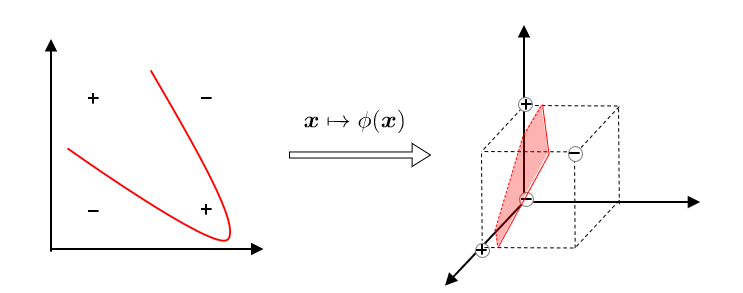
核支持向量机
设样本 $x$ 映射后的向量为 $\phi(x)$ ,则对偶化后的支持向量机为
\[f(x)=w^T\phi(x)+b=\sum\limits_{i=1}^m a_iy_i\phi(x_i)^T\phi(x)+b\]基本想法:不显式地设计核映射,而是设计核函数
\[\kappa(x_i,x_j)=\phi(x_i)^T\phi(x_j)\]Mercer定理(充分非必要):只要一个对称函数所对应的核矩阵半正定,则它就能作为核函数来使用
\[K= \begin{bmatrix} \kappa(x_1,x_1) & \kappa(x_1,x_2) & \dots & \kappa(x_1,x_m)\\ \kappa(x_2,x_1) & \kappa(x_2,x_2) & \dots & \kappa(x_2,x_m)\\ \vdots & \vdots & & \vdots\\ \kappa(x_m,x_1) & \kappa(x_m,x_2) & \dots & \kappa(x_m,x_m)\\ \end{bmatrix}\]常用的核函数

核函数注意事项:
- 核函数选择称为SVM最大变数
- 经验:文本数据使用线性核,情况不明使用高斯核
- 核函数的基本性质
- 核函数线性组合仍为核函数
- 核函数的直积仍为核函数
软间隔与正则化
现实中,很难确定合适的核函数使得训练样本在特征空间中线性可分;同时一个线性可分的结果也很难判断是否由过拟合造成
引入软间隔的概念,允许支持向量机在某些样本上不满足约束
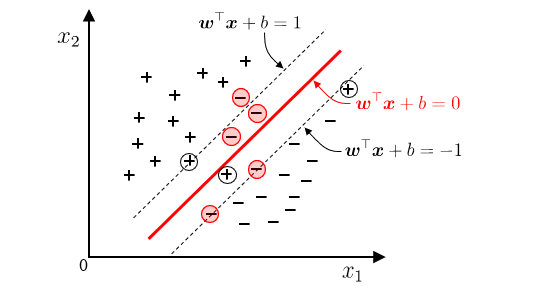
基本想法:最大化间隔的同时,让不满足约束的样本尽可能少
\[\min\limits_{w,b}\frac{1}{2}\Vert w\Vert^2+ C\sum\limits_{i=1}^m l_{0/1} (y_i(w^T\phi(x_i)+b)-1)\\ l_{0/1}(z)= \left\{ \begin{aligned} & 1\quad z<0\\ & 0\quad others \end{aligned} \right.\]正则化常数 $C>0$ ,如果 $C\rightarrow \infty$,则等价于要求所有的样本点都分类正确,否则就允许一部分极少的样本分类错误
存在的问题:0/1损失函数非凸、非连续、不易优化
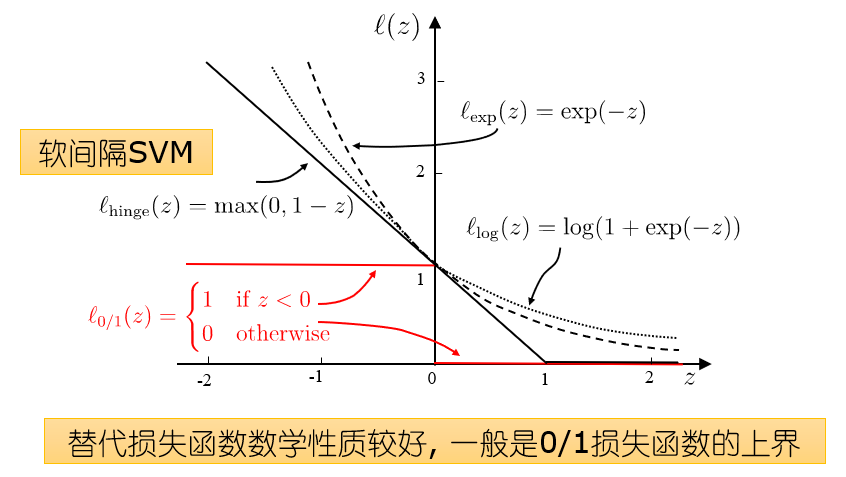
软间隔支持向量机
原始问题
\[\min\limits_{w,b}\frac{1}{2}\Vert w\Vert^2+C\sum\limits_{i=1}^m\max(0,1-y_i(w^Tx_i+b))\]引入松弛变量(slack variable) $\xi$
\[\min\limits_{w,b,\xi_i}\frac{1}{2}\Vert w\Vert^2+C\sum\limits_{i=1}^{m}\xi_i\\ s.t.\quad y_i(w^Tx_i+b)\ge 1-\xi_i\\ \xi_i\ge 0,i=1,2,\dots,m\]每个样本都对应一个松弛变量 $\xi$ ,用以表征该样本不满足约束 $y_if(x_i)\ge 1$ 的程度
求解软间隔问题
构造拉格朗日函数
\[L(w,b,\alpha,\xi,\mu)=\frac{1}{2}\Vert w\Vert+ C\sum\limits_{i=1}^{m}\xi_i+ \sum\limits_{i=1}^{m}\alpha_i(1-\xi_i-y_i(w^Tx_i+b)) -\sum\limits_{i=1}^{m}\mu_i\xi_i\\ s.t.\quad a_i\ge 0,\mu_i\ge 0\]分别对变量求导,并令其为0,得到
\[\left\{ \begin{aligned} & w=\sum\limits_{i=1}^m\alpha_iy_ix_i\\ & 0=\sum\limits_{i=1}^m\alpha_iy_i\\ & C=\alpha_i+\mu_i \end{aligned} \right.\]软间隔支持向量机KKT条件
\[\left\{ \begin{aligned} & \alpha\ge 0,\mu\ge 0\\ & y_if(x_i)-1+\xi_i\ge 0\\ & \alpha(y_if(x_i)-1+\xi_i)=0\\ & \xi_i\ge 0,\mu_i\xi_i=0 \end{aligned} \right.\]

- hinge损失有一块“平坦”的零区域,使得支持向量机的解具有稀疏性
- 对率损失是光滑的递减函数,不能导出类似支持向量的概念,因此对率回归的解依赖于更多的训练样本,其预测开销更大
正则化
支持向量机学习模型的更一般形式
\[\min\limits_f \Omega f(x)+C\sum\limits_{i=1}^ml(f(x_i),y_i)\]即最小化结构风险(描述模型的某些性质)和经验风险(描述模型与训练数据的契合程度)
通过替换上面的两部分,可以得到许多其他的学习模型
- 对数几率回归(logistic regression)
- 最小绝对收缩选择算子(LASSO)
正则化可以理解为一种惩罚函数,对不希望的结果施加惩罚,从而使得优化过程趋向于希望目标;从贝叶斯估计的角度看,正则化项可认为是提供了模型的先验概率
$L_p$ 范数(norm)是常用的正则化项
- 二范数倾向于参数向量的分量取值尽可能均衡,即非零分量个数尽量稠密
- 一范数倾向于参数向量的分量取值尽可能稀疏,即非零分量个数尽量少
支持向量回归
传统回归模型例如线性回归模型,基于模型输出和真实输出的距离来计算损失,当且仅当模型输出和真实输出完全相同时,损失才为零;支持向量回归(Support Vector Regression,SVR)假设模型能够容忍模型输出和真实输出之间最多 $\epsilon$ 的偏差
特点:允许模型输出和实际输出区间存在 $2\epsilon$ 的偏差
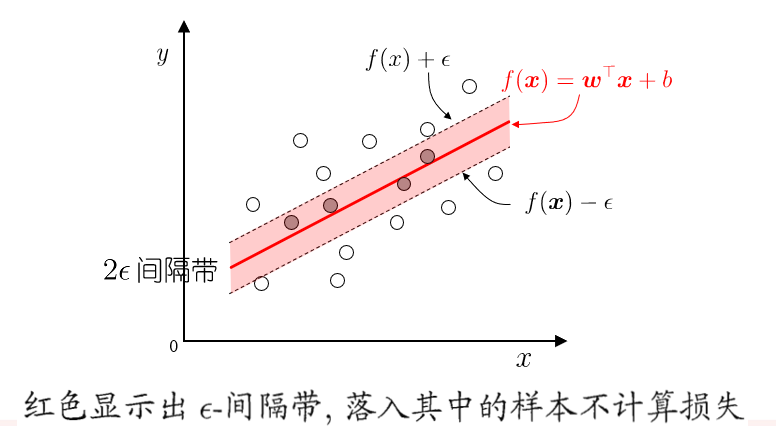
落入中间 $2\epsilon$ 间隔带的样本不计算损失,从而使得模型获得稀疏性
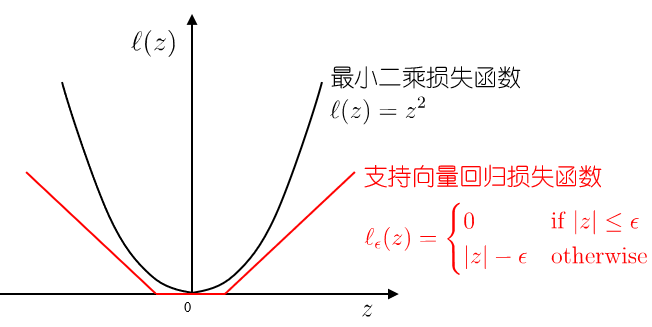
支持向量回归形式化
原始问题
\[\min\limits_{w,b,\xi_i,\hat{\xi_i}} \frac{1}{2}\Vert w\Vert^2+ C\sum\limits_{i=1}^m(\xi_i+\hat{\xi}_i)\\ s.t.\left\{ \begin{aligned} & y_i-(w^T\phi(x_i)+b)\le\epsilon+\xi_i,\\ & y_i-(w^T\phi(x_i)+b)\ge-\epsilon-\hat{\xi}_i,\\ & \xi_i\ge 0,\hat{\xi_i}\ge 0 \end{aligned} \right.\]对偶问题
\[\min\limits_{\alpha,\hat{\alpha}} \frac{1}{2}\sum\limits_{i=1}^m\sum\limits_{j=1}^m (\alpha_i-\hat{\alpha_i})(\alpha_j-\hat{\alpha_j}) \kappa(x_i,x_j)+\sum\limits_{i=1}^m (\alpha_i(\epsilon-y_i)+\hat{\alpha_i}(\epsilon+y_i))\\ s.t.\quad \sum\limits_{i=1}^m(\alpha_i-\hat{\alpha_i})=0,\\ 0\le \alpha_i\le C,0\le \hat{\alpha_i}\le C\]核方法
从 SVM 和 SVR 的对偶形式可以看出,学到的模型总是可以表示成核函数的线性组合
更一般的结论(表示定理):对于任意单调增函数 $\Omega$ 和任意非负损失函数 $l$ ,优化问题
\[\min\limits_{h\in\mathbb{H}} F(h)=\Omega(\Vert h\Vert_\mathbb{H})+l(h(x_1),\dots,h(x_m))\]的解总是可以写成 $h^*=\sum\limits_{i=1}^m\alpha_i\kappa(\cdot,x_i)$
核线性判别分析
通过表示定理可以得到很多线性模型的核化版本
- 核SVM
- 核LDA
- 核PCA
核LDA:将样本映射到高维特征空间,然后再此特征空间做线性判别分析
总结
- 支持向量机最大间隔思想
- 对偶问题及其解的稀疏性
- 通过向高维空间映射解决线性不可分的问题
- 引入“软间隔”缓解特征空间线性不可分的问题
- 将支持向量的思想应用到回归问题上得到支持向量回归
- 将核方法推广到其他学习模型
数学基础
- 机器学习必知必会:凸优化
- 理解凸优化
- KKT条件,原来如此简 理论+算例实践
- Karush-Kuhn-Tucker (KKT)条件
- 真正理解拉格朗日乘子法和 KKT 条件
- MIT 18.065—机器学习中的矩阵方法05 正定矩阵和半正定矩阵
- 浅谈「正定矩阵」和「半正定矩阵」
- 对偶理论:基本概念札记
- 机器学习数学:拉格朗日对偶问题
- SVM的一个快速求解方法(SMO算法)
- 机器学习算法实践-SVM中的SMO算法
- 机器学习里的 kernel 是指什么?