聚类任务

在”无监督学习”任务中研究最多、应用最广

聚类目标：将数据集的样本划分为若干个通常不相交的子集（“簇”，cluster）

聚类既可以作为一个单独的过程（寻找数据内在的分布结构），也可作为分类等其他学习任务的前驱过程

形式化描述

假定样本集 $D={x_1,\dots,x_m}$ 包含m个无标记样本，每个样本 $x_i=(x_{i1},\dots,x_{in})$ 是一个n维的特征向量，聚类算法将样本集D划分为k个不相交的簇 ${C_l\vert l=1,\dots.k}$

相应地，用 $\lambda_i\in {1,\cdots,k}$ 表示样本 $x_j$ 的“簇标记”（cluster label），即 $x_i\in C_{\lambda_j}$ ，聚类的结果可以用包含m个元素的簇标记向量 $\lambda_{\lambda_1.\dots,\lambda_m}$ 表示

性能度量

聚类性能度量，也称为聚类“有效性指标”（validity index）

同一个簇内的样本尽可能相似，不同簇的样本尽可能不同。聚类结果的”簇内相似度“（intra-cluster similarity）高，且”簇间相似度“（inter-cluster similarity）低，聚类效果好

聚类性能度量

外部指标（external index）：将聚类结果和某个”参考模型“（reference model）比较
内部指标（internal index）：直接考察聚类结果而不参考任何模型

对数据集合 $D={x_1,\dots,x_m}$ ，假定通过聚类划分得到的簇划分为 $C={C_1,\dots,C_k}$ 参考模型给出的簇划分为 $C^={C_1^\text{},\dots,C_s^\text{*}}$ ，

相应地，令 $\lambda,\lambda^{}$ 分别表示 $C,C^{}$ 对应的簇标记向量

\[a=\vert SS\vert,SS=\{(x_i,x_j)\vert\lambda_i=\lambda_j,\lambda_i^*=\lambda_j^*,i<j\}\\ b=\vert SD\vert,SD=\{(x_i,x_j)\vert\lambda_i=\lambda_j,\lambda_i^*\ne\lambda_j^*,i<j\}\\ c=\vert DS\vert,DS=\{(x_i,x_j)\vert\lambda_i\ne\lambda_j,\lambda_i^*=\lambda_j^*,i<j\}\\ d=\vert DD\vert,DD=\{(x_i,x_j)\vert\lambda_i\ne\lambda_j,\lambda_i^*\ne\lambda_j^*,i<j\}\\\]

外部指标

Jaccard系数（Jaccard coefficient，JC）

\[JC=\frac{a}{a+b+c}\]

FM指数（fowlkes and mallows index，FMI）

\[FMI=\sqrt{\frac{a}{a+b}\cdot\frac{a}{a+c}}\]

Rand指数（rand index，RI）

\[RI=\frac{2(a+b)}{m(m-1)}\]

$[0,1]$ 区间内，越大越好

内部指标

考虑聚类结果簇划分 $C={C_1,\dots,C_k}$ ，定义簇内样本间的平均距离

\[avg(C)=\frac{2}{\vert C\vert(\vert C\vert-1)}\sum_{1\le i\le j\le\vert C\vert}dist(x_i,x_j)\]

簇内样本间的最远距离

\[diam(C)=\max_{1\le i\le j\le\vert C\vert}dist(x_i,x_j)\]

簇间样本的最近距离

\[d_{min}(C)=\min_{x_i\in C_i,x_j\in C_j}dist(x_i,x_j)\]

簇中心点间的距离

\[d_{cen}(C)=dist(\mu_i,\mu_j)\]

DB指数（Davies-bouldin index，DBI）：越小越好

\[DBI=\frac{1}{k}\sum\limits_{i=1}^k\max\limits_{j\ne i}(\frac{avg(C_i)+avg(C_j)}{d_{cen}(\mu_i,\mu_j)})\]

Dunn指数（Dunn index，DI）：越大越好

\[DI=\min\limits_{1\le i\le k}\{\min\limits_{j\ne i}(\frac{d_{min}(C_i,C_j)}{\max_{1\le l\le k}diam(C_l)})\}\]

距离计算

距离度量的性质：非负性、同一性、对称性、三角不等式

常用距离：

闵可夫斯基距离（minkowski distance）：

\[dist(x_i,x_j)=(\sum\limits_{k=1}^n\vert x_{ik}-x_{jk}\vert^p)^{\frac{1}{p}}\]

$p=2$ ：欧氏距离（Euclidean distance）

$p=1$ ：曼哈顿距离（Manhattan distance）

属性介绍：

连续属性（continuous attribute）
离散属性（categorical attribute）
有序属性（ordinal attribute）
无序属性（non-ordinal attribute）

距离度量

Value Difference Metric，VDM（处理无序属性）

令 $m_{u,a}$ 表示属性u上取值为a的样本数， $m_{u,a,i}$ 表示在第i个样本簇中属性u上取值为a的样本数，k为样本数，则属性u上两个离散值a和b之间的VDM距离为

\[VDM_p(a,b)=\sum\limits_{i=1}^k\vert \frac{m_{u,a,i}}{m_{u,a}}-\frac{m_{u,b,i}}{m_{u,b}}\vert^p\]

MinkovDMp（处理混合属性，即连续+离散）

\[MinkovDM_p(x_i,x_j)=(\sum\limits_{u=1}^{n_c}\vert x_{iu}-x_{ju}\vert^p+\sum\limits_{u=n_c+1}^{n}VDM_p(x_{iu},x_{ju}))^{\frac{1}{p}}\]

加权距离（样本中不同属性的重要性不同时）：

\[dist(x_i,x_j)=(\omega_1\cdot\vert x_{i1}-x_{j1}\vert^p+\cdots+\omega_n\cdot\vert x_{in}-x_{jn}\vert^p)^{\frac{1}{p}}\]

省流：VDM对离散属性进行距离度量，对比同一簇内属性的不同取值分布上的差异，分布越相似，属性值距离越近

原型聚类

原型聚类也称为“基于原型的聚类”（prototype-based clustering），算法假设聚类结构能够通过一组原型刻画

算法过程：算法对原型进行初始化，再对原型迭代更新求解

几种著名的原型聚类算法：k均值算法、学习向量化算法、高斯混合聚类算法

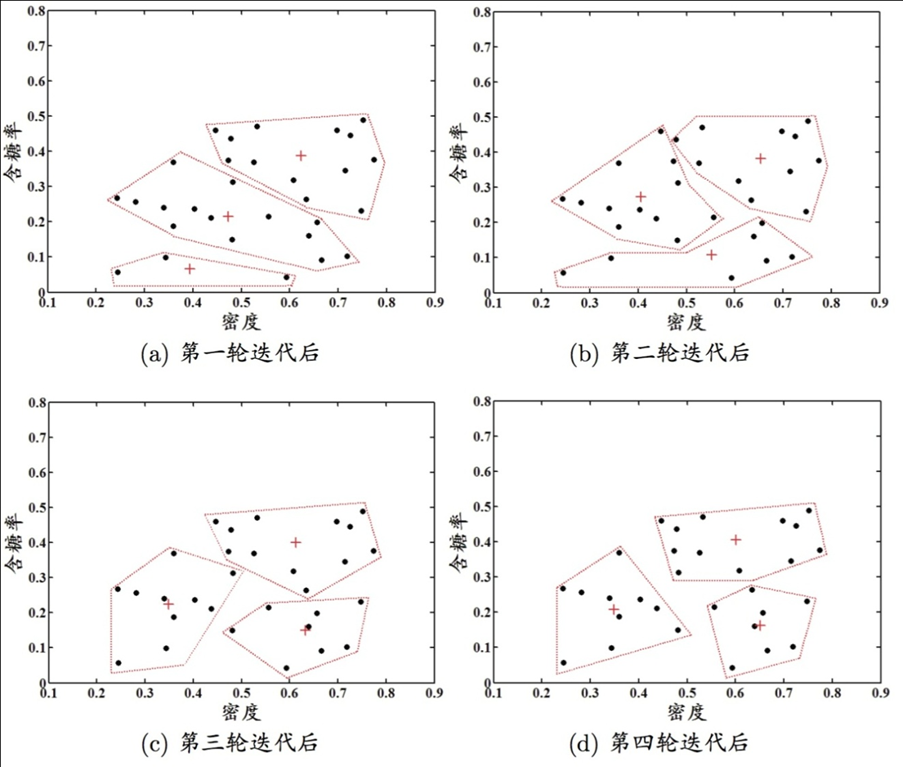
k均值算法

给定数据集 $D={x_1,\dots,x_m}$ ，k均值算法对聚类所得簇划分 $C={C_1,\dots,C_k}$ ，簇均值向量 $\mu={\mu_1,\dots,\mu_k}$ ，最小化平方误差

\[E=\sum\limits_{i=1}^k\sum\limits_{x\in C_j}\Vert x-\mu_i\Vert_2^2\]

E值一定程度上刻画了簇内样本围绕簇均值向量的紧密程度，E值越小，则簇内样本相似度越高。

学习向量化

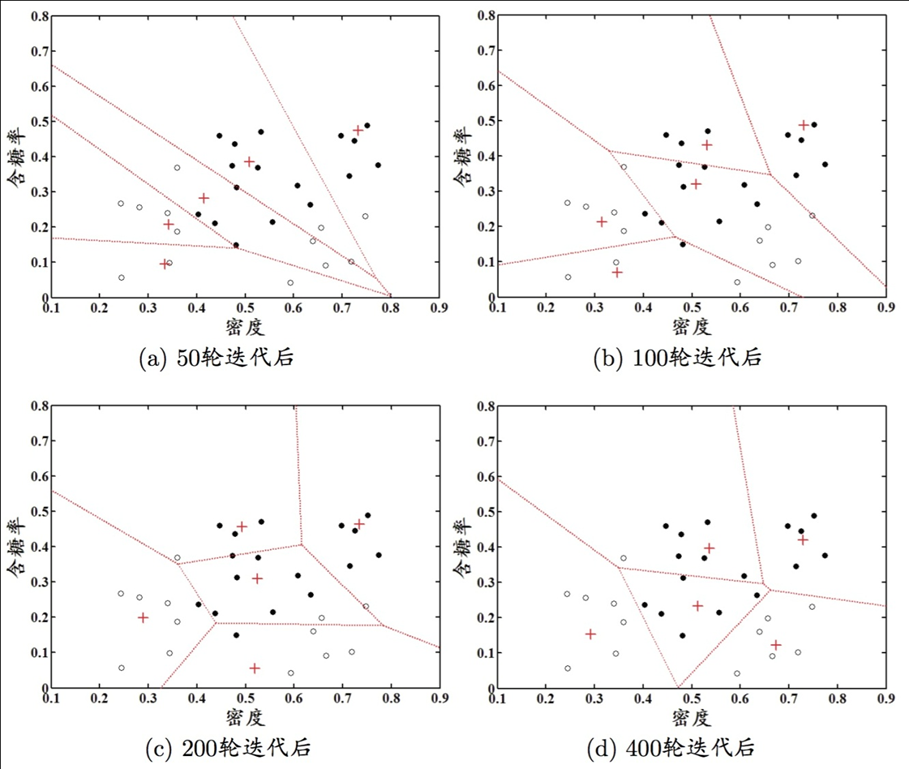
学习向量化（learning vector quantization，LVQ），和一般聚类算法不同，LVQ假设数据样本带有类别标记，学习过程中利用样本的监督信息来辅助聚类

给定样本集 $D={(x_1,y_1),\dots,(x_m,y_m)}$ ，LQV的目标是学得一组n维原型向量 ${p_1,\dots,p_q}$ ，每个原型向量代表一个聚类簇。

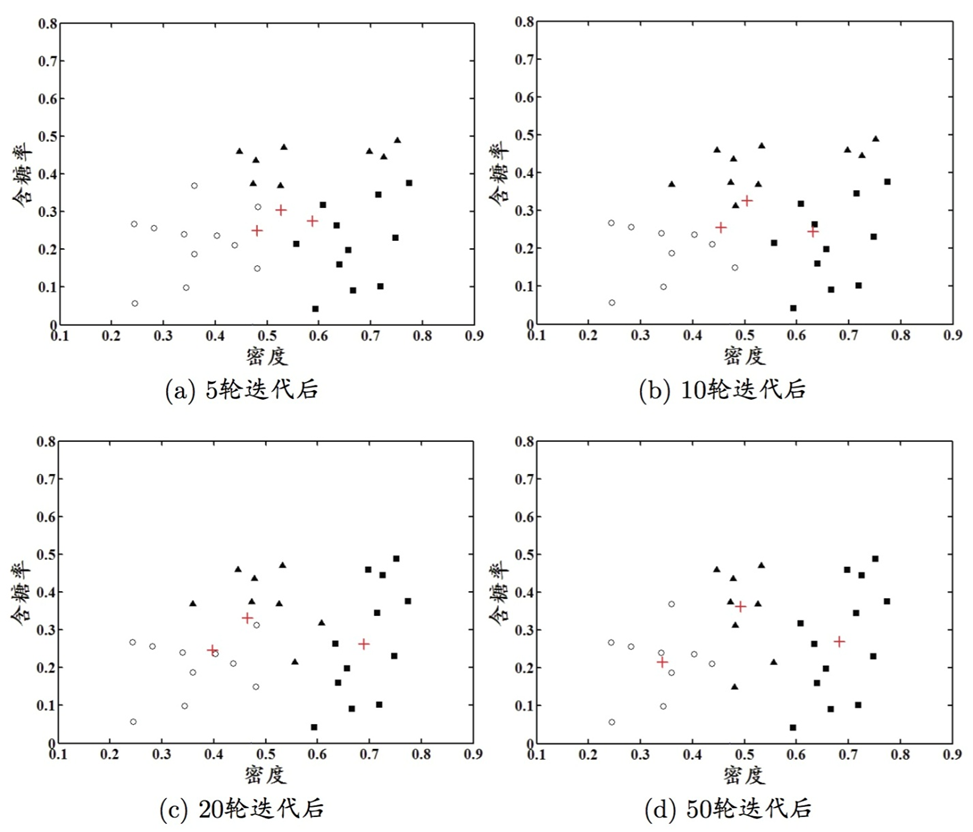
高斯混合聚类

和k均值、LVQ用原型向量来刻画聚类结构不同，高斯混合聚类（mixture-of-gaussian）采用概率模型来表达聚类原型

对n维样本空间中的随机向量x，若x服从高斯分布，其概率密度函数为：

\[p(x)=\frac{1}{(2\pi)^{\frac{n}{2}}\vert\Sigma\vert^\frac{1}{2}}e^{-\frac{1}{2}(x-\mu)^T\Sigma^{-1}(x-\mu)}\]

其中 $\mu$ 是n维均值向量， $\Sigma$ 是 $n\times n$ 的协方差矩阵，也可将概率密度记为 $p(x\vert \mu,\Sigma)$

高斯混合分布的定义

\[P_M(x)=\sum\limits_{i=1}^k\alpha_i p(x\vert\mu_i,\Sigma_i)\]

该分布由k个混合分布组成，其中 $\alpha$ 是“混合系数”

假设样本的生成过程由高斯混合分布给出：

首先，根据混合系数定义的先验分布选择高斯混合成份，其中 $\alpha_i$ 为选择第i个混合成分的概率
然后，根据被选择的混合成分的概率密度函数进行采样，从而生成相应的样本

模型求解

最大化对数似然

\[\begin{aligned} LL(D) &=\ln(\prod\limits_{j=1}^m p_M(x_j))\\ &=\sum\limits_{j=1}^m\ln(\sum\limits_{k=1}^k P(\mu_i,\Sigma_i)\cdot p(x_j\vert \mu_i,\Sigma_i))\\ &=\sum\limits_{j=1}^m\ln(\sum\limits_{k=1}^k\alpha_i\cdot p(x_j\vert \mu_i,\Sigma_i)) \end{aligned}\\ \frac{\partial LL(D)}{\partial\mu_i}=0 \Rightarrow \mu_i=\frac{\sum_{i=1}^m \gamma_{ji}x_j}{\sum_{i=1}^m \gamma_{ji}}\\ \frac{\partial LL(D)}{\partial\Sigma_i}=0 \Rightarrow \Sigma_i=\frac{\sum_{i=1}^m \gamma_{ji}(x_j-\mu_i)(x_j-\mu_i)^T}{\sum_{i=1}^m \gamma_{ji}}\\ \alpha_i'=\frac{\sum_{j=1}^m \gamma_{ji}}{m}\\ \gamma_{ji}=p_{\mathcal{M}}(z_j=i\vert x_j)\]

其中 $\gamma_{ji}$ 表示样本 $x_j$ 属于高斯分布i的后验概率

密度聚类

密度聚类也称为“基于密度的聚类”（density-based clustering），算法假设聚类结构能通过样本分布的紧密程度来确定。

通常情况下，密度聚类算法从样本密度的角度来考察样本之间的可连接性，并给予可连接样本不断扩展聚类簇来获得最终的聚类结果。

DBSCAN算法

DBSCAN算法：基于一组“邻域”参数 $(\epsilon,MinPts)$ 来刻画样本分布的紧密程度

基本概念：

$\epsilon$ 邻域：区域内的样本与样本 $x_j$ 距离不大于 $\epsilon$
核心对象：邻域内至少包含MinPts个样本的样本点
密度直达：样本 $x_j$ 在核心对象 $x_i$ 的邻域内
密度可达：存在样本序列 $p_1,\dots,p_n$ ，相邻样本点密度直达，间隔样本点则密度可达
密度相连：两个样本点可由另一个样本点密度可达，那么这两个样本点密度相连

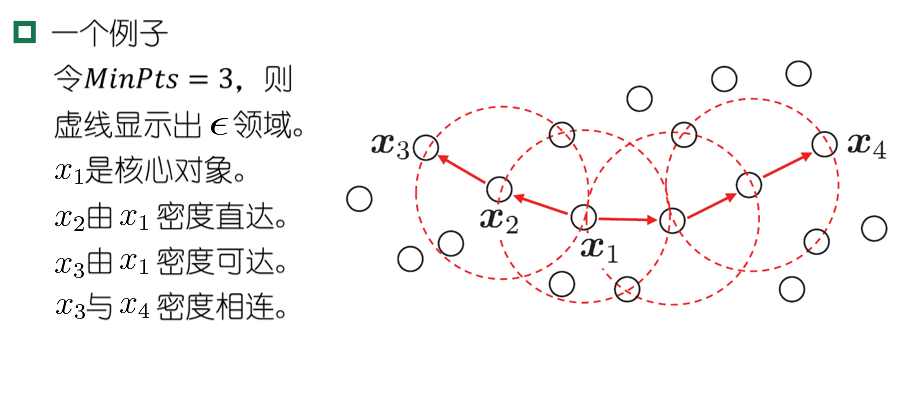
对“簇”的定义：由密度可达关系导出的最大密度相连的样本集合

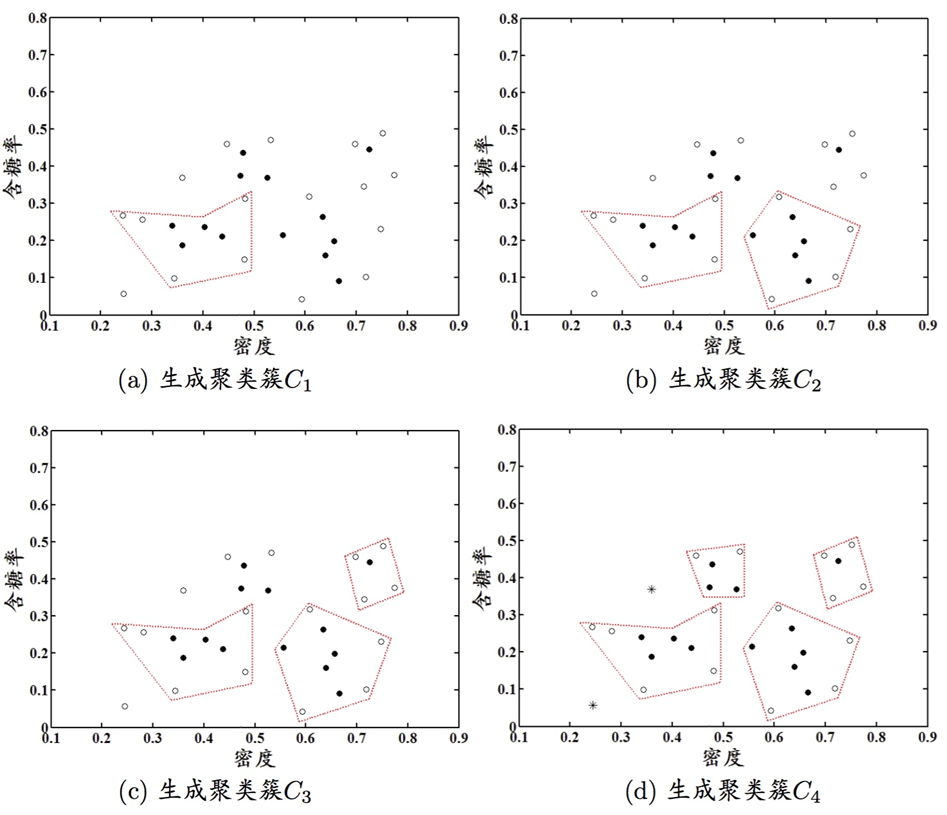
层次聚类

层次聚类视图在不同层次对数据集进行划分，从而形成树形的聚类结构。可以自底向上聚合，也可以自顶向下分拆

AGNES算法

AGNES（自底向上的层次聚类）：

将每个样本看作一个初始聚类簇
运行的每一步中找到距离最近的两个聚类簇合并
不断重复，直到达到预设的聚类簇个数

这里两个聚类簇之间的距离，可以有三种度量方式

最小距离：

\[d_{min}(C_i,C_j)=\min\limits_{x\in C_i,z\in C_j}dist(x,z)\]

最大距离：

\[d_{min}(C_i,C_j)=\max\limits_{x\in C_i,z\in C_j}dist(x,z)\]

平均距离：

\[d_{avg}(C_i,C_j)=\frac{1}{\vert C_i\vert\vert C_j\vert} \sum\limits_{x\in C_i}\sum\limits_{z\in C_j}dist(x,z)\]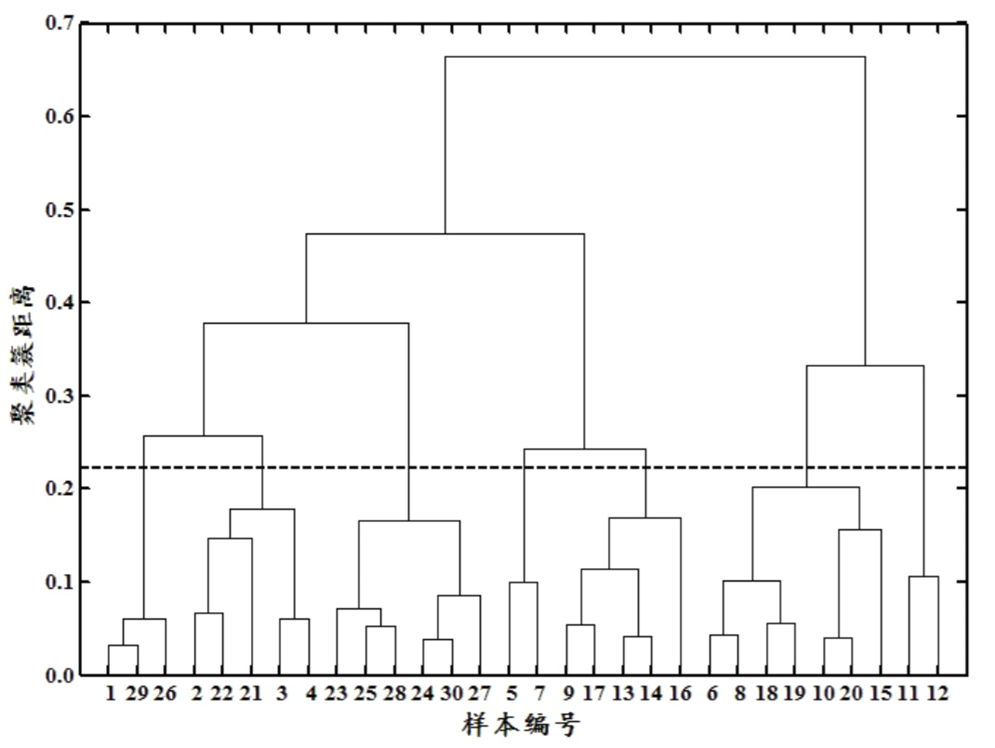

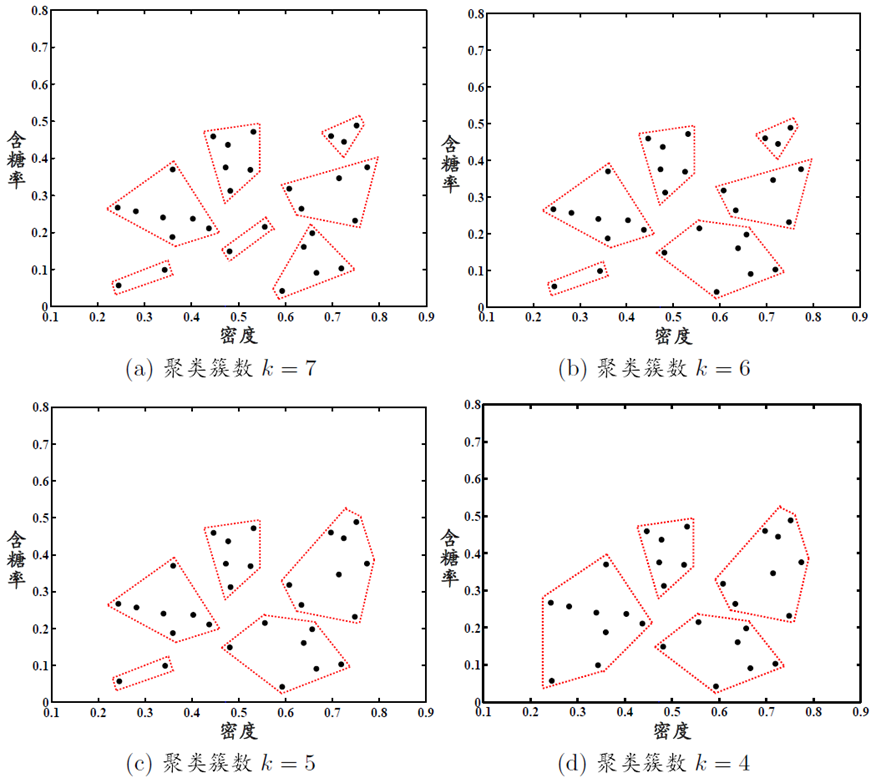
省流：聚类需要距离度量，原型聚类分为k均值、学习向量化、高斯混合模型，密度聚类有DBSCAN，层次聚类有AGNES

机器学习——聚类