决策树模型
决策树基于”树“结构进行决策
- 内部节点:某个属性上的”测试“(test)
- 分支:对于测试的一种可能结果(属性的某个取值)
- 叶节点:预测结果
学习过程:通过对训练样本的分析来确定”划分属性“
预测过程:将测试示例从根节点开始,沿着划分属性所构成的判定测试序列下行,知道叶节点
决策树算法历史:
-
CLS(Concept Learning System):第一个决策树算法
-
ID3:使决策树收到关注、称为机器学习主流技术的算法
-
C4.5:最常用的决策树算法
-
CART(Classification and Regression Tree):可用于回归任务
-
RF(Random Forest):基于决策树的集成学习算法
基本流程
策略:分支
三种停止条件:
- 当前节点包含的样本全属于同一类别,无需划分
- 当前属性集为空,或是所有样本在所有属性上取值相同,无法划分
- 当前节点包含的样本集合为空,不能划分

信息增益(information gain)
信息熵
信息熵(entropy):度量样本集合”纯度“的指标
假定当前样本集合D的第k类样本所占的比例 $p_k$ ,则D的信息熵定义为
\[Ent(D)=-\sum\limits_{k=1}^{\vert y\vert}p_k\log_2{(p_k)}\]信息熵越小,数据集D的纯度越高
约定: $p=0,则p\log_2(p)=0$
信息增益计算
离散属性a的取值: ${a^1,a^2,…,a^V}$
$D^v$ :数据集D在属性a上取值为 $a_v$ 的样本集合
以属性a对数据集D进行划分所得到的信息增益为:
\[Gain(D,a)=Ent(D)-\sum\limits_{v=1}^{V} \frac{\vert D^v\vert}{\vert D\vert}Ent(D^v)\]即划分前的信息增益减去划分后的信息增益,第v个分支权重表示样本越多越重要
增益率
信息增益:对”可取值数目较多“的属性有所偏好
增益率:
\[Gain_{ratio}(D,a)=\frac{Gain(D,a)}{Ⅳ(a)}\]其中
\[Ⅳ(a)=-\sum\limits_{v=1}^V\frac{\vert D^v\vert}{\vert D\vert}\log_2\frac{\vert D^v\vert}{\vert D\vert}\]属性a的可能取值数目越多(即V越大),则 $Ⅳ(a)$ 的值越大
启发式算法: 从候选划分属性中找出信息增益高于平均水平的,在从中选取增益率最高的
缺点:对取值数目少的属性有所偏好
基尼指数(gini index)
\[Gini(D)=\sum\limits_{k=1}^{\vert y\vert} \sum\limits_{k'\ne k}p_{k}p_{k'} =1-\sum\limits_{k=1}^{\vert y\vert}p_k^2\]反映了从D中随机抽取两个样例,其类别标记不一致的概率
Gini(D)基尼指数越小,数据集D的纯度越高
属性a的基尼指数:
\[Gini_index(D,a)=\sum\limits_{v=1}^V \frac{\vert D^v\vert}{\vert D\vert}Gini(D^v)\]在侯选属性集合中,选取使得划分后基尼指数最小的属性
划分选择vs剪枝
研究表明:划分选择的各种准则,对决策树的尺寸有较大的影响,但对泛化性能的影响有限,信息增益和基尼指数产生的结果差别不大
剪枝方法和程度对决策树的泛化性能影响更为显著,剪枝(pruning)用于解决决策树的过拟合问题
基本策略:
- 预剪枝(pre-pruning):提前终止某些分支的生长
- 后剪枝(post-pruning):生成一棵完全树,然后”回头“剪枝
剪枝过程中需要评估剪枝前后决策树的优劣,假定使用”留出法“
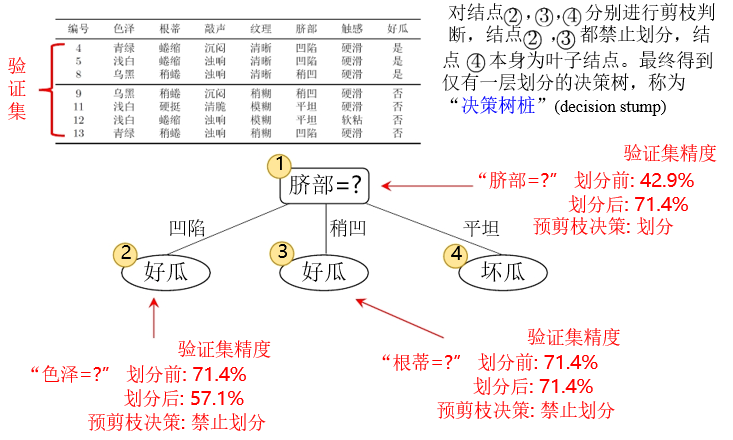
预剪枝
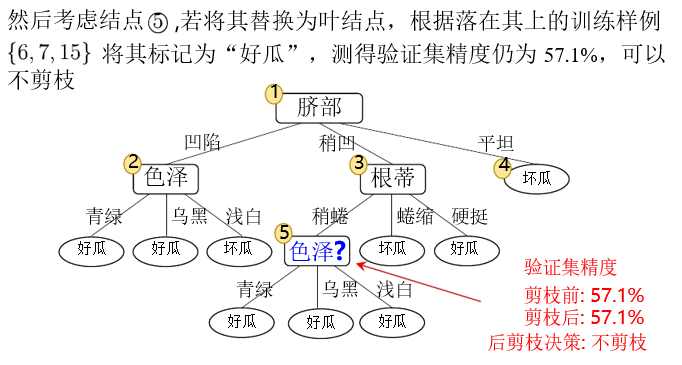
后剪枝
预剪枝vs后剪枝
- 时间开销:
- 训练时间:预剪枝降低,后剪枝增加
- 测试时间:预剪枝降低,后剪枝增加
- 过/欠拟合风险:
- 预剪枝:过拟合风险降低,欠拟合风险增加
- 后剪枝:过拟合风险降低,欠拟合风险基本不变
- 泛化性能:后剪枝优于预剪枝
连续值
基本思路:连续属性离散化
常见做法:二分法(bi-partition) - n个属性值可形成n-1个候选划分 - 然后将它们当作n-1个离散属性值处理
缺失值
遇到属性值”缺失”(missing)现象,如果仅使用无缺失样例,对数据造成极大的浪费
基本思路:样本赋权,权重划分
\[Gain(D,a)=\rho \times Gain(\hat{D},a)\]$\rho$ 表示无缺失值样例占比, $\hat{D}$ 表示
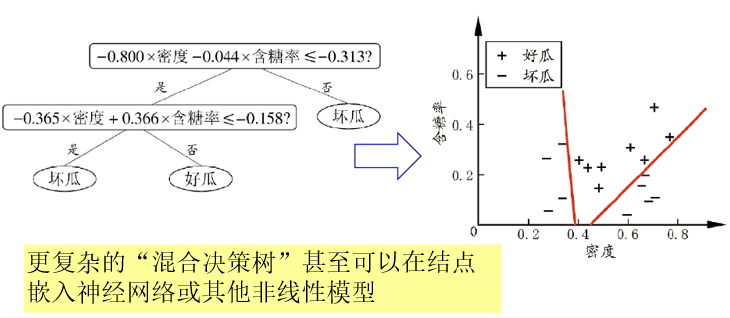
轴平行vs倾斜
从“树”到“规则”
- 一棵“决策树”对应一个“规则集”
- 从根节点到叶节点的分支路径对应于一条“规则”
IF-THEN 的规则改善了模型的可理解能力,进一步提升泛化能力
单变量决策树:在每个非叶节点仅考虑一个划分属性,产生“轴平行”分类面
缺点:当学习任务对应的分类边界很复杂,需要多段划分才能很好近似
多变量决策树
多变量决策树:每个非叶节点不仅考虑一个属性
例如“斜决策树”(oblique decision tree)不是为每个非叶节点寻找最优属性划分,而是建立一个线性分类器