线性模型

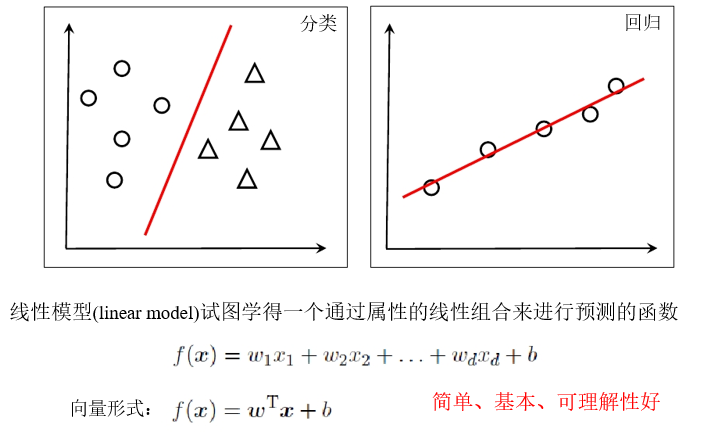
线性回归

离散属性的处理：如果有“序”（order），则连续化；否则，转化为k维向量

令均方误差最小，有

\[(w^*,b^*)=\mathop{\arg\min}\limits_{(w,b)}\sum_{i=1}^m (y_i-wx_i-b)^2\]

对 $E_{(w,b)}$ 进行最小二乘参数估计

多元线性回归

令 $\hat{w}={w;b},w\in\mathbb{R}^{n\times 1},X\in\mathbb{R}^{m\times n},y\in\mathbb{R}^{m\times 1}$

同样采用最小二乘法求解，有

\[w^*=\mathop{\arg\min}\limits_{w}(y-X\hat{w})^T(y-X\hat{w})\]

令 $E_w$ 对 $w$ 求导等于零，有

\[\frac{\partial E_w}{\partial w}=2X^T(X\hat{w}-y)\]

如果 $X^TX$ 满秩或正定，则

\[\hat{w}=(X^TX)^{-1}X^Ty\]

如果 $X^TX$ 不满秩，则可以解出多个 $w$

此时需要借助归纳偏好，或者引入正则化（regularization）

广义线性模型

一般形式：

\[y=g^{-1}(w^Tx+b)\]

其中 $g^{-1}$ 是单调可微的联系函数（link function）

类似于非线性回归做变化得到线性回归

二分类任务

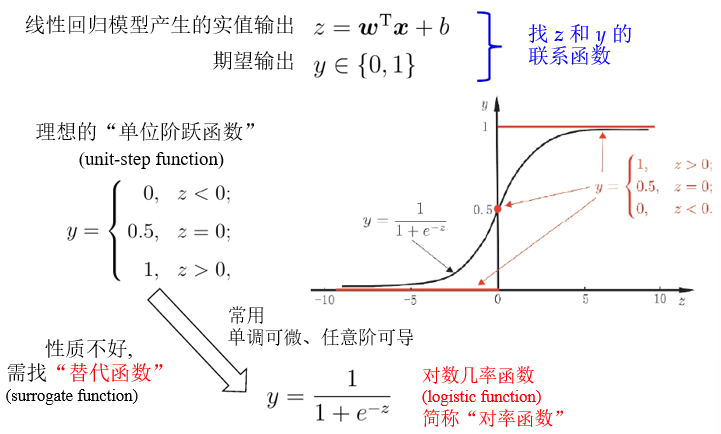
对率回归

以对率函数为联系函数：

\[y=\frac{1}{1+e^{-z}}\Rightarrow z=\ln\frac{y}{1-y}\\ y=\frac{1}{1+e^{-z}}\quad 变为\quad y=\frac{1}{1+e^{-(w^Tx+b)}} \\ 几率：\quad \ln\frac{y}{1-y}=w^Tx+b\]

几率（odds）：反映 $x$ 作为正例的相对可能性

线性模型就这样从回归模型推演为分类模型

无需实现假设数据分布
可以得到类别的近似概率预测
可以直接用现有的数值优化算法求取最优解

假设一个二维空间，对正反类有标记样本，寻找一个线性模型将其划分，正类的模型输出z大于零，负类的模型输出z小于零。y表示样本根据线性模型输出z被划分为正类的概率，当z>0时y>0.5，大概率为正类；当z<0时y<0.5，大概率为反类。离模型决策边界越远，分类正确概率越大。

求解思路

将 $y$ 当作后验概率估计 $P(y=1\vert x)$ ，则

\[\ln\frac{y}{1-y}=w^Tx+b \quad 可写为 \\ \ln\frac{P(y=1\vert x)}{P(y=0\vert x)}=w^Tx+b\]

使用极大似然法（maximum likelihood method）

给定数据集 ${(x_i,y_i)}_{i=1}^m$ ，最大化“对数似然函数”：

\[\ell(w,b)=\sum\limits_{i=1}^{m}\ln p(y_i\vert x_i;w,b)\]

令 $\beta=(w,b),\hat{x}=(x;1)$ ，则 $w^Tx+b$ 简写为 $\beta^T\hat{x}$

再令

\[p_1(\hat{x_i};\beta)=p(y=1\vert \hat{x};\beta) =\frac{e^{\beta^T\hat{x}}}{1+e^{\beta^T\hat{x}}} \\ p_0(\hat{x_i};\beta)=p(y=0\vert \hat{x};\beta) =1-p_1(\hat{x_i};\beta) =\frac{1}{1+e^{\beta^T\hat{x}}} \\ p(y_i\vert x_i;w,b)=y_ip_1(\hat{x_i};\beta)+ (1-y_i)p_0(\hat{x_i};\beta)\]

于是

\[\max \ell(w,b)=\sum\limits_{i=1}^{m}\ln p(y_i\vert x_i;w,b) \Longleftrightarrow \\ \min \ell(\beta)=\sum\limits_{i=1}^{m} (-y_i\beta^T\hat{x_i}+\ln(1+e^{\beta^T\hat{x_i}}))\]

高阶可导连续凸函数，可使用经典数值优化算法，如梯度下降法、牛顿法

省流：广义线性模型做分类任务的核心，使用了对率回归表示后验概率，通过极大似然法构造凸函数优化目标；做回归任务的核心，通过最小化距离构造优化目标。

线性判别分析

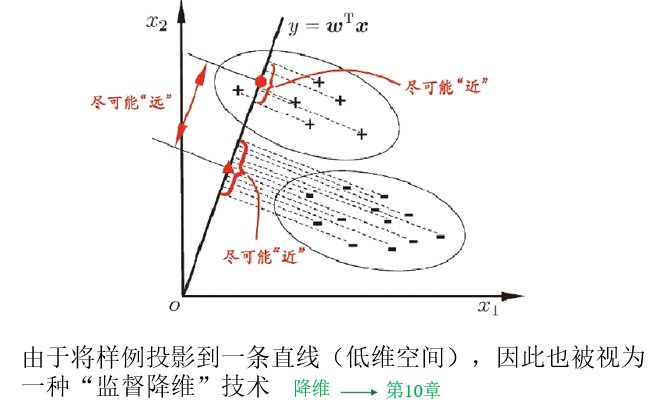
给定数据集 ${(x_i,y_i)}^m_{i=1}$

第i类示例的集合 $X_i$

第i类示例的均值向量 $\mu_i$

第i类示例的协方差矩阵 $\Sigma_i$

两类样本的中心在直线上的投影 $w^T\mu_0,w^T\mu_1$

两类样本的协方差 $w^T\Sigma_0w,w^T\Sigma_1w$

同类样例的投影点尽可能接近，即 $w^T\Sigma_0w+w^T\Sigma_1w$ 尽可能小

异类样例的投影点尽可能远离，即 $\Vert w^T\mu_0-w^T\mu_1\Vert_2^2$ 尽可能大

于是，最大化

\[J=\frac{\Vert w^T\mu_0-w^T\mu_1\Vert_2^2}{w^T\Sigma_0w+w^T\Sigma_1w} = \frac{w^T(\mu_0-\mu_1)(\mu_0-\mu_1)^Tw}{w^T(\Sigma_0+\Sigma_1)w}\]

LDA目标

类内散度矩阵（within-class scatter matrix）

\[S_w=\Sigma_0+\Sigma_1 = \sum\limits_{x\in X_0}(x-\mu_0)(x-\mu_0)^T+ \sum\limits_{x\in X_1}(x-\mu_1)(x-\mu_1)^T\]

类间散度矩阵（between-class scatter matrix）

\[S_b=(\mu_0-\mu_1)(\mu_0-\mu_1)^T\]

LDA的目标：最大化广义瑞利商（generalized Rayleigh quotient）

\[J=\frac{w^TS_bw}{w^TS_ww}\]

LDA求解

最大化广义瑞利商等价形式为

\[\min\limits_{w}-w^TS_bw \\ s.t.\quad w^TS_ww=1\]

运用拉格朗日乘子法，有 $S_bw=\lambda S_ww$

$S_bw$ 的方向恒为 $\mu_0-\mu_1$ ，不妨令 $S_bw=\lambda(\mu_0-\mu_1)$

解得 $w=S_w^{-1}(\mu_0-\mu_1)$

其中通过奇异值分解 $S_w=U\Sigma V^T$

然后 $S_w^{-1}=V\Sigma^{-1}U^T$

省流：LDA类似于降维，将带标签的数据点映射和线性模型向量做内积进行映射，求得类间中心向量距离和类内协方差。LDA的目的是找到一个线性模型，最大化类间距离，同时约束类内散度之和单位化。拉格朗日求解对应优化问题，得到线性模型。

推广到多类

假定有N个类

全局散度矩阵

\[S_t=\sum\limits_{i=1}^{N}\sum\limits_{x\in X_i}=(x-\mu)(x-\mu)'\]

类内散度矩阵

\[S_w=\sum\limits_{i=1}^{N}\sum\limits_{x\in X_i}(x-\mu_i)(x-\mu_i)'\]

类间散度矩阵

\[S_b=\sum\limits_{i=1}^{N}m_i(\mu_i-\mu)(\mu_i-\mu)'\]

其中第i类样本个数为$m_i$

$S_t=S_w+S_b$

多分类学习

拆解法：将一个多分类任务拆分为若干个二分类任务求解

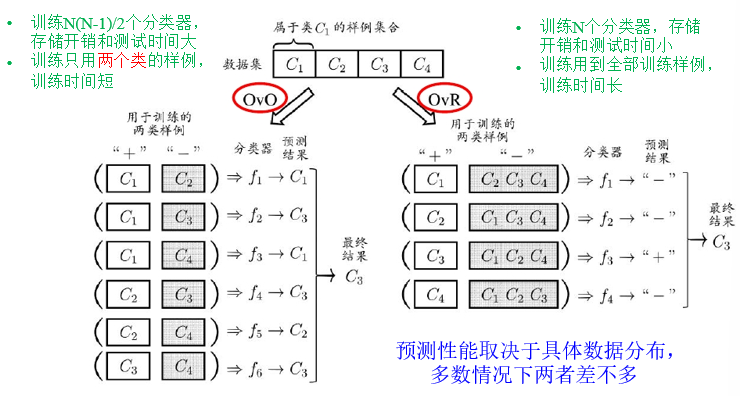
多对多：将若干类作为真类，若干类作为反类，对类别进行编码

编码：将N个类别做M次划分，每次划分将一部分类作为正类，一部分类作为反类
M个二类任务：每个类对应M位编码
解码：测试样本交给M个分类器预测
和预测结果编码距离最小的类编码为最终结果

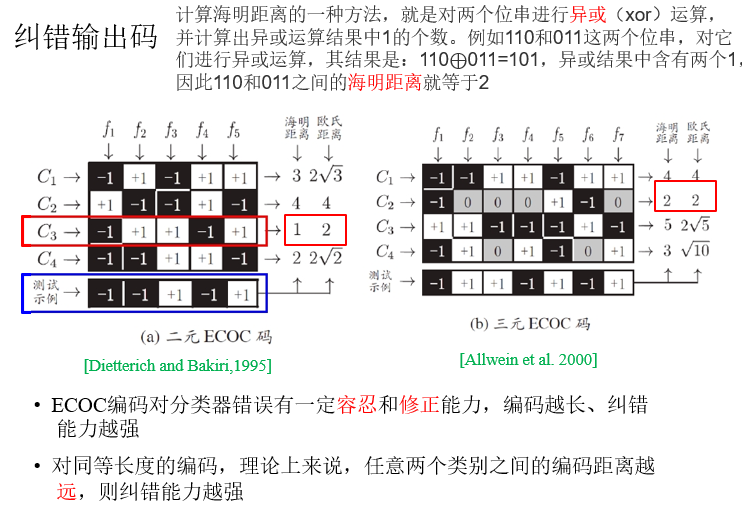
类别不平衡

不同类别的样本比例差别很大，”小类“往往更重要

类别不平衡学习方法

过采样（oversampling）：例如SMOTE
欠采样（undersampling）：EasyEnsemble
阈值移动（threshold-moving）

机器学习——线性模型