神经网络
神经网络是一个具有适应性的简单单元组成的广泛并行互联的网络,神经网络学得的知识蕴含在连接权重和阈值中
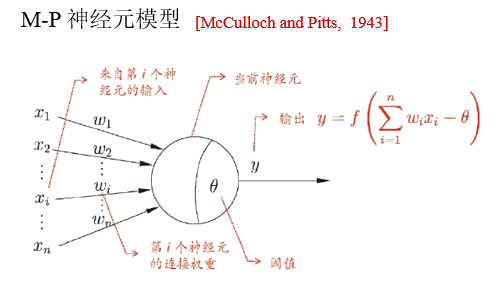
激活函数
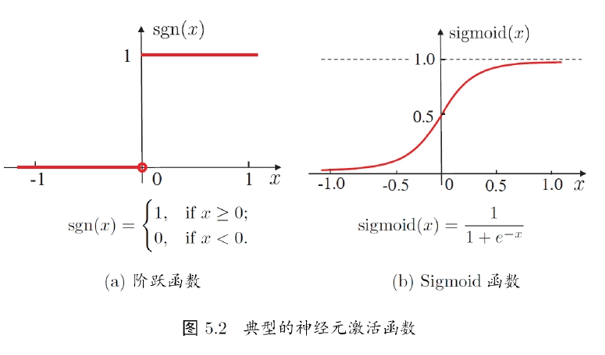
- 理想激活函数是阶跃函数,0表示抑制神经元而1表示激活神经元
- 阶跃函数具有不连续性、不光滑等不好的性质,常用的是Sigmoid函数
多层前馈网络结构
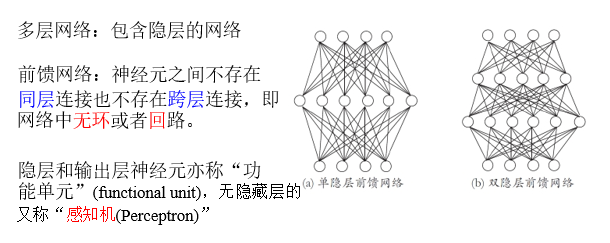
多层前馈网络有强大的表示能力:只需要足够多神经元的隐层,多层前馈网络就能以任意精度逼近任意复杂度的连续函数
误差逆传播算法(BP)
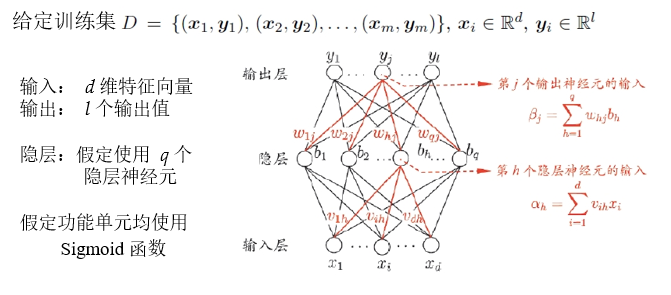
$v_{ih},w_{hj}$ 分别是输入层-隐层、隐层-输出层连接权重
$\alpha_h,\beta_j$ 分别是隐层、输出层未激活输出
$\gamma_h,\theta_j$ 分别是隐层、输出层未激活输出偏置
$x_i,b_h,y_j$ 分别是输入层、隐层、输出层激活函数输出
BP算法推导
对于训练用例 $(x_k,y_k)$ ,假定网络实际输出为 $\hat{y}_k=(\hat{y}_1^k,\dots,\hat{y}_l^k)$ ,则输出层第j个神经元输出:
\[\hat{y}_j^k=f(\beta_j-\theta_j)\]则网络在该训练用例上的均方误差为
\[E_k=\frac{1}{2}\sum\limits_{j=1}^l(\hat{y}_{j}^k-y_j^k)^2\]需要通过学习确定的参数数目为: $(d+l+1)q+l$
BP是一个迭代学习算法,在迭代的每一轮中采用如下误差修正:
\[v\leftarrow v+\Delta v\]BP算法基于梯度下降策略,以目标的负梯度方向对参数调整,以 $w_{hj}$ 为例,对误差 $E_k$ ,给定学习率 $\eta$ ,有:
\[\Delta w_{hj}=-\eta \frac{\partial E_k}{\partial w_{hj}}\]注意到 $w_{hj}$ 先影响到 $\beta_j$ ,然后再影响到 $\hat{y}_j^k$ ,最后再影响到 $E_k$ ,通过链式法则:
\[\frac{\partial E_k}{\partial w_{hj}}= \frac{\partial E_k}{\partial \hat{y}_j^k}\cdot \frac{\partial \hat{y}_j^k}{\partial \beta_j}\cdot \frac{\partial \beta_j}{\partial w_{hj}}\\\]对 $sigmoid(x)=\frac{1}{1+e^{-x}}$ ,有 $f’(x)=f(x)(1-f(x))$ ,求导很方便,所以有
\[\begin{aligned} g_j &=-\frac{\partial E_{k}}{\partial \hat{y}_j^k}\cdot \frac{\partial \hat{y}_j^k}{\partial \beta_j}\\ &=-(\hat{y}_j^k-y_j^k)f'(\beta_j-\theta_j)\\ &=-(\hat{y}_j^k-y_j^k)\hat{y}_j^k(1-\hat{y}_j^k) \end{aligned}\]又因为
\[\frac{\partial \beta_j}{\partial w_{hj}}=b_h\]于是
\[\begin{aligned} \Delta w_{hj} &=-\eta \frac{\partial E_k}{\partial \Delta w_{hj}}\\ &=\eta g_{j}b_h\\ &=\eta(\hat{y}_j^k-y_j^k)\hat{y}_j^k(1-\hat{y}_j^k)b_h \end{aligned}\]类似地有
\[\Delta\theta_j=-\eta g_j\\ \Delta v_{ih}=\eta e_h x_i\\ \Delta \gamma_h=-\eta e_h\]其中
\[\begin{aligned} e_h &=-\frac{\partial E_{h}}{\partial b_h}\cdot \frac{\partial b_n}{\partial \alpha_{h}}\\ &=-\sum\limits_{j=1}^l \frac{\partial E_{h}}{\partial \beta_j}\cdot \frac{\partial \beta_j}{\partial b_n}f'(\alpha_h-\gamma_h)\\ &=\sum\limits_{j=1}^l w_{hj}g_{j} f'(\alpha_h-\gamma_h)\\ &=\sum\limits_{j=1}^l w_{hj}g_{j} b_h(1-b_h) \end{aligned}\]
标准BP算法和积累BP算法
\[E_k=\sum\limits_{j=1}^l (\hat{y}_j^{(k)}-y_j^{(k)})^2\\ E=\frac{1}{m}\sum\limits_{k=1}^m E_k= \frac{1}{m}\sum\limits_{k=1}^m\sum\limits_{j=1}^l (\hat{y}_j^{(k)}-y_j^{(k)})^2\]标准BP算法:
- 每次针对单个训练样例更新权重与阈值
- 参数更新频繁,不同样例可能抵消,需要多次迭代
积累BP算法:
- 其优化目标是最小化整个训练集上的累计误差
- 读取整个训练集一遍才对参数进行更新,参数更新频率较低
很多任务中,积累误差下降到一定程度后,进一步下降会非常缓慢,这时标准BP算法会有较好的解,在训练集非常大时效果更明显
缓解过拟合
BP算法常常导致过拟合
主要策略:早停(early stopping)和正则化(regularization)
早停:
- 若训练误差连续a轮变化小于b,则停止训练
- 使用验证集:若训练误差降低、验证误差升高,则停止训练
正则化:
- 在误差目标函数中增加一项描述网络复杂度
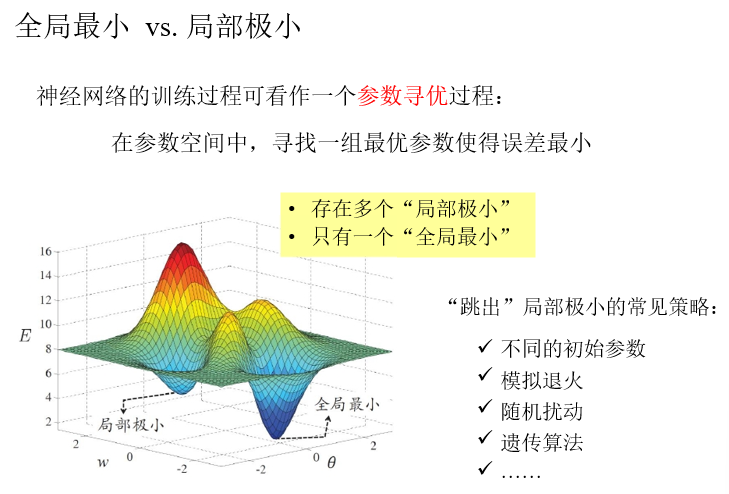
不同的初始参数:
- 以多组不同参数值初始化神经网络,按照标准方法训练后,取误差最小的解作为最终参数。相当于从多个不同的初始点开始搜索,这样可能陷入不同的局部最小,从中选择最有可能接近全局最小的结果
模拟退火(simulated annealing):
- 模拟退火在每一步以一定概率选择比当前解更差的结果,从而有助于跳出局部最小。每步迭代的过程中,接收”次优解“的概率要随着时间的推移逐渐降低,从而保证算法的稳定
梯度下降:
- 随机梯度下降法在计算梯度时加入了随机因素,即使陷入局部极小点,它计算出来的梯度仍不可能为零,有机会跳出局部极小继续搜索
其他神经网络模型
RBF神经网络
RBF(radial basis function):径向基函数
其中q为隐层神经元个数, $c_i,w_i$ 分别是第i个隐层神经元所对应的中心和权重, $\rho(x_i,c_i)$ 为径向基函数
径向基函数是某种沿径向对称的标量函数,通常定义为样本x到数据中心c之间欧氏距离的单调函数,比如高斯径向基函数:
\[\rho(x,c_i)=e^{-\beta_i\Vert x-c_i\Vert^2}\]输出层是隐层神经元输出的线性组合
\[\phi(x)=\sum_{i=1}^q w_i\rho(x,c_i)\]训练:
- 确定神经元中心,常用方式包括随机采样、聚类
- 利用BP算法确定参数
SOM
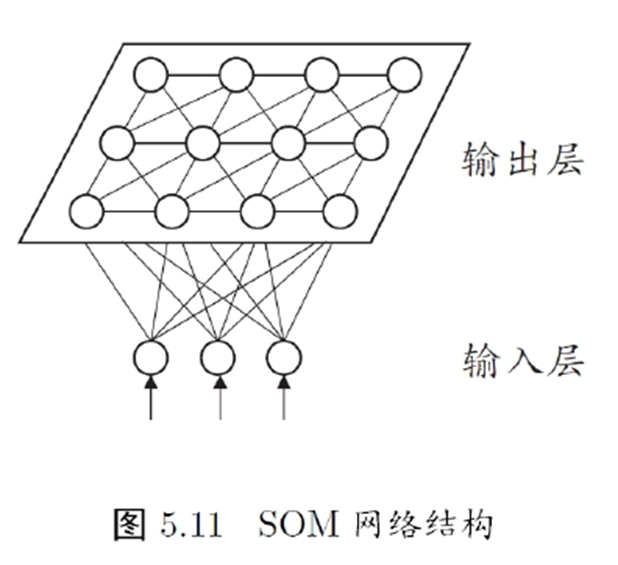
SMO网络中的输出神经元以矩阵方式排列在二维空间中,每个神经元都有一个权向量,网络在接收输入向量后,会确定输出层的获胜神经元,它决定了该输入向量在低维空间中的位置
- 竞争型的无监督神经网络
- 将高维数据映射到低维空间,高维空间中相似的样本点映射到网络输出层的邻近神经元
- 每个神经元拥有一个权向量
SMO的训练目标:为每个输出层神经元导出合适的权向量,以达到保持拓扑结构的目的
训练过程:
- 接收到一个训练样本后,每个输出层神经元计算该样本与自身携带的权向量之间的距离
- 距离最近的神经元成为竞争获胜者,称为最佳匹配单元(best matching unit)
- 最佳匹配单元和近邻神经元的权向量将被调整,使得权向量和当前输入样本的距离最小
- 不断迭代,直到收敛
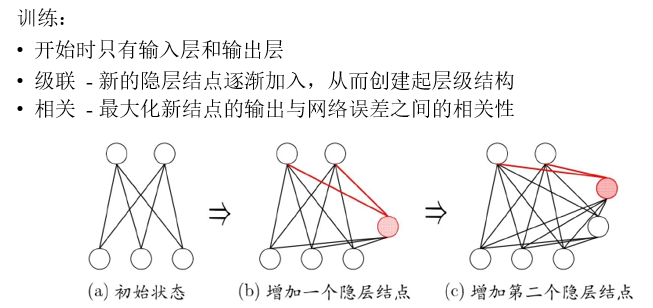
级联相关网络
构造性神经网络:将网络的结构也当作学习的目标之一,在训练的过程中找到适合数据的网络结构
级联相关网络(Cascade-Correlation)是结构自适应网络的重要代表
Elman网络
递归神经网络: RecurrentNN
- 网络中可以有环形结构,可以让一些神经元的输出反馈回来作为输入
- t时刻网络的输出状态:由t时刻的输入状态和t-1时刻的网络状态共同决定

常用诀窍(tricks)
- 预训练+微调
- 预训练:监督逐层训练,每次训练一层的隐节点
- 微调:对全网络进行微调训练,通常使用BP算法
可以视为将大量参数分组,对每组先找到较好的局部配置,再全局寻优
- 权共享
- 一组神经元使用相同的连接权值
- 减少需要优化的参数
- Dropout
- 每轮训练时随机选择一些隐节点令其权重不被更新
- 降低复杂度
- ReLU
- 将Sigmoid激活函数改为修正线性函数
- 求导容易,缓解梯度消失现象