绪论

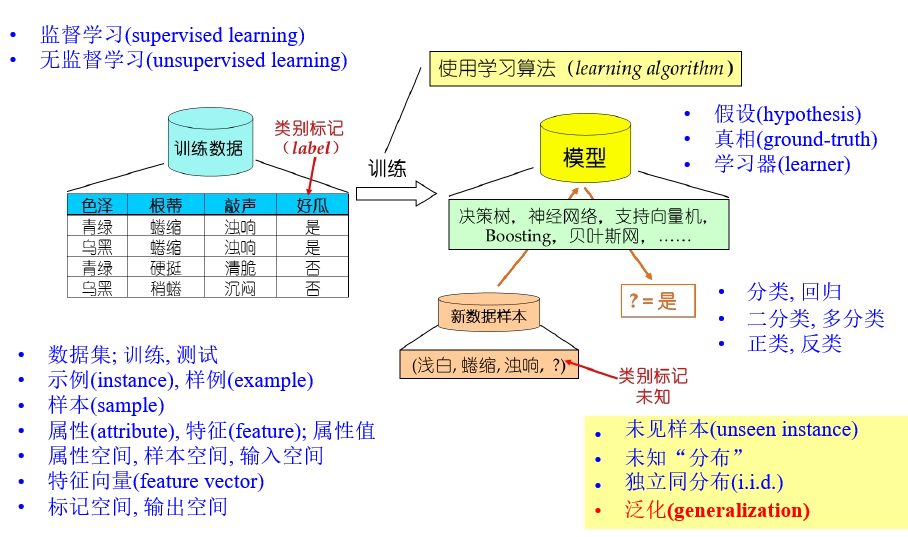
基本术语

学习过程：在所有假设hypothesis组成的空间中进行搜索的过程
版本空间（version space）：找到与训练集一致的假设集合
归纳偏好（inductive bias）：机器学习算法在学习的过程中对某种假设的偏好，任何一个有效的的机器学习算法必有其其偏好；一般遵循奥卡姆剃刀原则

学习算法的归纳偏好与否和问题本身匹配，大多数直接决定算法能否取得最好的性能！
泛化误差：在“未来”样本上的误差
经验误差：在训练集上的误差，也称为“训练误差”

模型选择（model selection）

三个关键问题：如何获得测试结果？如何评估性能优劣？如何判断实质差别？

评估方法

关键：如何获得测试集（test set）？

留出法（hold-out）

直接对数据集划分
- 保持数据分布一致（分层采样）
- 多次重复划分（100次随机划分）
- 划分比例适中（1/5~1/3）
交叉验证法（cross validation）

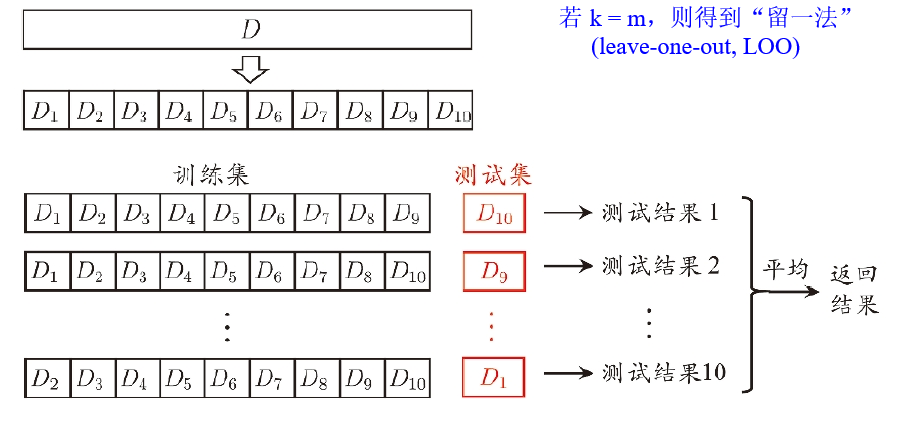
自助法（boostrap）

基于自助采样（boostrap sampling），有放回采样、可重复采样
- 约有36.8%的样本不出现，包外估计（out-of-bag estimation） $\lim\limits_{m\rightarrow\infty}(1-\frac{1}{m})^m=\frac{1}{e}$

算法参数：由人工设定，“超参数”
模型参数：有模型学习确定

性能度量

性能度量（performance measure）：衡量模型泛化能力的评价指标，反映了任务需求

什么样的模型是“好”的，不仅取决于算法和数据，还取决于任务需求

均方误差

回归任务常用均方误差

\[E(f,D)=\frac{1}{m}\sum\limits_{i=1}^m(f(x_i)-y_i)^2\]

错误率

\[E(f,D)=\frac{1}{m}\sum\limits_{i=1}^m\Pi(f(x_i)\ne y_i)\]

精度

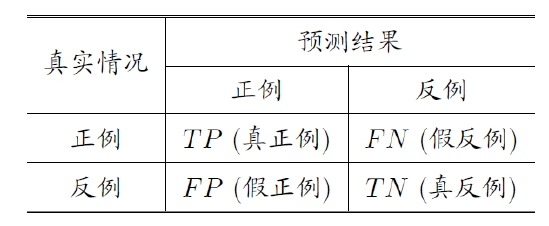
\[acc(f,D)=\frac{1}{m}\sum\limits_{i=1}^m\Pi(f(x_i)=y_i)=1-E(f,D)\]

混淆矩阵

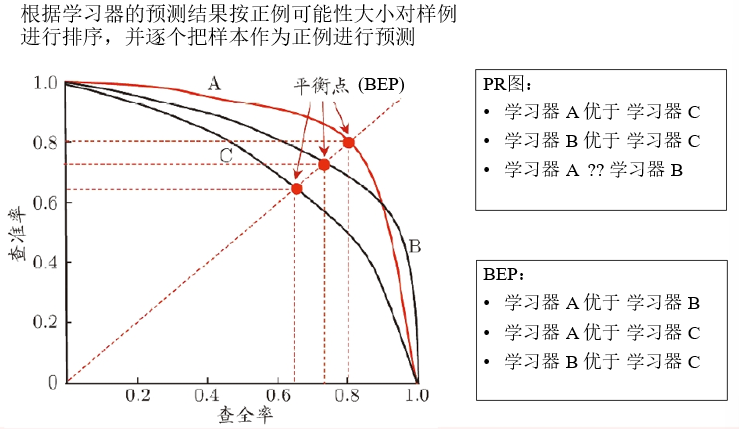
查准率：
\[P=\frac{TP}{TP+FP}\]
查全率
\[R=\frac{TP}{TP+FN}\]

PR图，BEP

F1

比BEP更常用的是F1度量

\[F1=\frac{2\times P\times R}{P+R}\]

如果对查准率/查全率有不同的偏好

\[F_\beta=\frac{(1+\beta^2)\times P\times R}{\beta^2\times P+R}\]

$\beta>1$ 查全率影响更大； $\beta<1$ 查准率影响更大

宏指标和微指标

若能得到多个混淆矩阵

宏（macro-）查准率、查全率、F1

\[macro\text{-}P=\frac{1}{n}\sum\limits_{i=1}^n P_i \\ macro\text{-}R=\frac{1}{n}\sum\limits_{i=1}^n R_i \\ macro\text{-}F=\frac{2\times macro\text{-}P\times macro\text{-}R}{macro\text{-}P+macro\text{-}R}\]

微（micro-）查准率、查全率、F1

\[micro\text{-}P=\frac{\overline{TP}}{\overline{TP}+\overline{FP}} \\ micro\text{-}R=\frac{\overline{TP}}{\overline{TP}+\overline{FN}} \\ micro\text{-}F=\frac{2\times micro\text{-}P\times micro\text{-}R}{micro\text{-}P+micro\text{-}R}\]

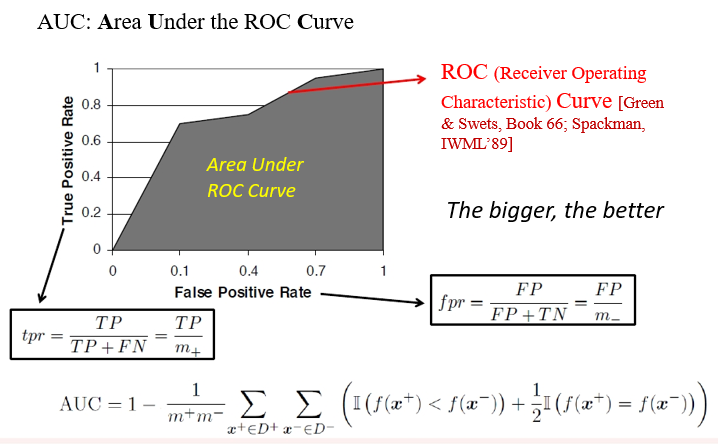
ROC，AUC

比较检验

在某种度量下取得评估结果后，不能直接比较判断优劣。因为测试性能不等于泛化性能，测试性能随着测试集的变化而变化，很多机器学习算法本身具有一定的随机性。机器学习得到的是“概率近似正确”。

机器学习的理论基础：PCA（probably approximately correct）

\[P(|f(x)-y|\le\varepsilon)\ge 1-\delta\]

统计假设检验

统计假设检验（hypothesis test）为学习器性能比较提供了重要依据：统计显著性

两学习器比较
- 交叉验证 $\tau$ 检验（基于成对 $\tau$ 检验）：k折交叉验证
- McNemar检验（基于列连表，卡方检验）
多学习器比较
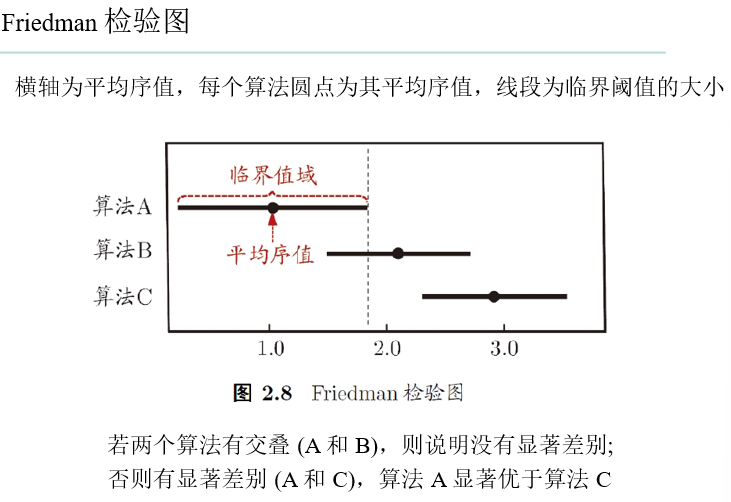
- Friedman+Nemenyi
  - Friedman检验（基于序值，F检验；判断“是否都相同“）
  - Nemenyi后续检验（基于序值，进一步判断两两差别）

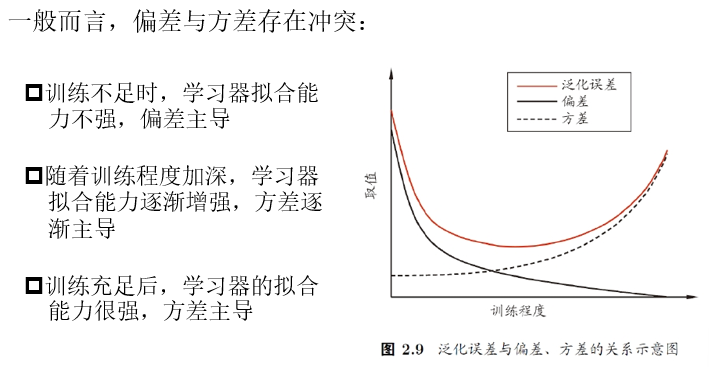
误差来源

偏差-方差分解

偏差-方差分解（bias-variance decomposition）：对回归任务，泛化误差可以通过”偏差-方差”拆解为

\[E(f,D)=bias^2(x)+var(x)+\varepsilon^2 \\ bias^2(x)=(\overline{f}(x)-y)^2 \\ var(x)=\mathbb{E}_D[f(x,D)-\overline{f}(x)^2] \\ \varepsilon^2=\mathbb{E}_D[(y_D-y)^2]\]

$bias^2(x)$ ：期望输出与真实输出的差别

$var(x)$ ：同样大小的训练集的变动，所导致的性能变化

$\varepsilon^2$ ：表达当前任务上任何学习算法所能达到的期望泛化误差下界

泛化性能是由学习算法的能力、数据的充分性、学习任务本身的难度共同决定

机器学习——模型的评估和选择

绪论