关系数据理论

数据依赖是现实世界属性相互联系的抽象

数据依赖是语义的体现

函数依赖是为了建立唯一性索引和更好的数据关系

数据依赖的类型

函数依赖：唯一确定的关系

某个属性集决定另一个属性集时，称另一属性集依赖于该属性集；

构造函数依赖传递
多值依赖：不能唯一确定的关系

函数依赖不能表示属性值之间的一对多联系

没有直接联系但有间接的联系称为多值依赖的数据依赖

函数依赖是多值依赖的特殊情况。

数据依赖对关系模式的影响

好的关系模式不会发生插入异常、删除异常（数据丢失）、更新异常，而且数据冗余（数据重复）尽可能少。

不好的模式是由于模式中存在不合理的数据依赖，所以我们要通过分解关系模式来消除其中不合适的数据依赖（规范化）。

函数依赖

函数依赖闭包，

当一个表T可以分解为若干表，这些表自然连接后可以得到T，这种分解为无损分解。

若对于R(U)的任意一个可能的关系r，r中不可能存在两个元组在X上的属性值相等，而在Y上的属性值不等，则称 “X函数确定Y”或 “Y函数依赖于X”，记作X→Y；

若X→Y，并且Y→X,则记为X←→Y。

平凡函数依赖与非平凡函数依赖

如果$X→Y$，但$Y\nsubseteq X$，则称$X→Y$是非平凡的函数依赖
如果$X→Y$，但$Y\subseteq X$,则称$X→Y$是平凡的函数依赖

举例：

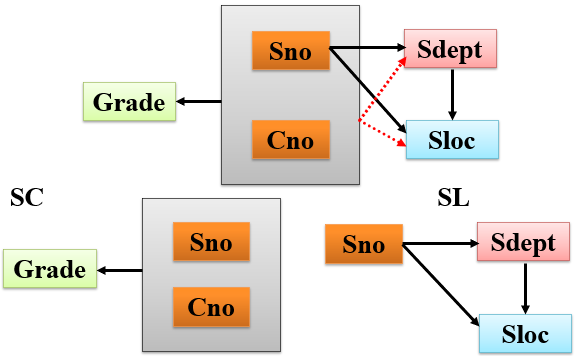
在关系SC(Sno, Cno, Grade)中，
非平凡函数依赖： (Sno, Cno) → Grade
平凡函数依赖：     (Sno, Cno) → Sno      (Sno, Cno) → Cno

我的理解是不自己依赖于自己，非平凡的函数依赖有意义

完全函数依赖与部分函数依赖

定义：在关系模式$R(U)$中，如果$X→Y$，并且对于X的任何一个真子集X’，都有$X’ \rightarrow Y$,则称Y完全函数依赖于X，记作$X \stackrel{F}{\rightarrow} Y$。
若$X→Y$，但Y不完全函数依赖于X，则称Y部分函数依赖于X，记作

$X \stackrel{P}{\rightarrow} Y$ 。

我的理解是不可再分，属性集合不冗余

传递函数依赖

在关系模式R(U)中，如果$X→Y$，$Y→Z$，且$Y\subsetneq X$，$Y\nrightarrow X$，则称Z传递函数依赖于X。

举例：

在关系Std(Sno，Sdept，Mname)中，有：
      Sno → Sdept，Sdept → Mname
      Mname传递函数依赖于Sno

间接的函数依赖

候选码

https://www.cnblogs.com/wasi-991017/p/12611009.html

k是关系模式的一个属性或者属性组合，如果可以表示唯一元组且码的子集不能表示唯一元组,则K是R的一个候选码（Candidate Key)。如果关系模式中有多个候选码，则选其中一个作为主码。

超级码、候选码（最小超级码）、主码（任选一个候选码）、主属性（出现在候选码中的属性）、非主属性、外部码

主属性：候选码中包含的属性
非主属性：不包含在任何一个候选码中的属性
全码：整个属性组都是码
外部码：R中的属性或者属性组X并非R的码，但是X是另一个关系模式的码，则X是R的外部吗

通过画有向图，确定候选码

范式

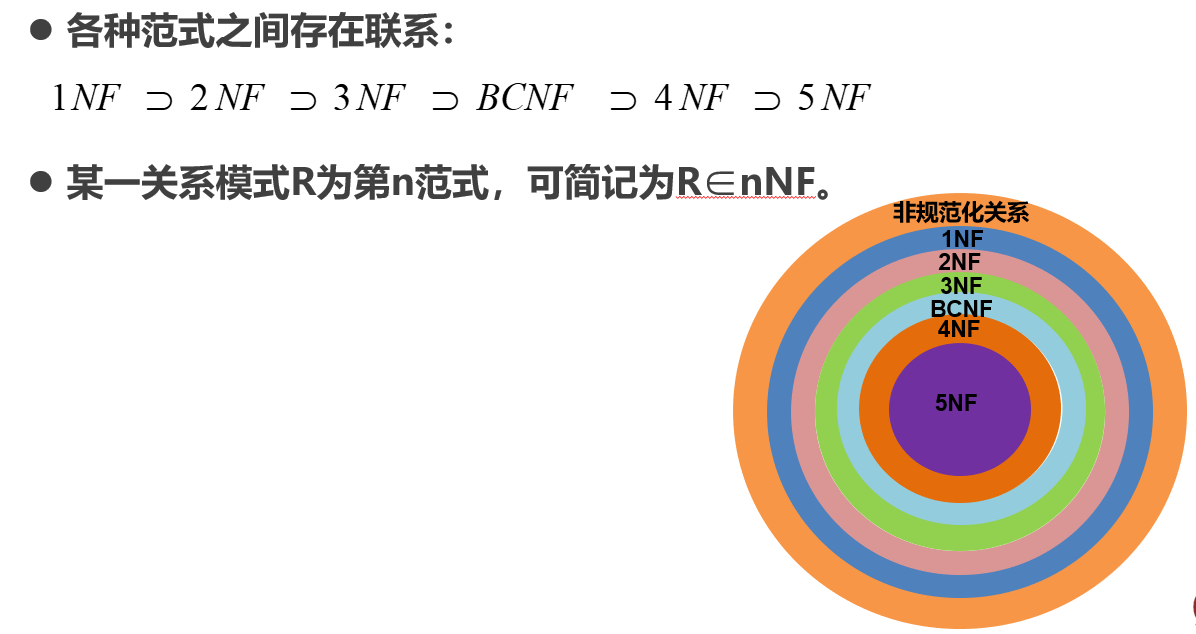
1NF

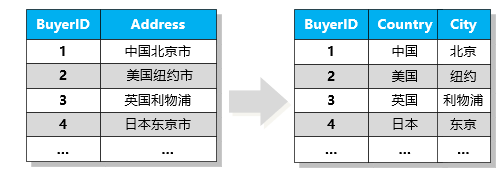
关系模式中所有属性都是不可再分的基本数据项

原子属性、不可分，关系数据库一定满足1NF

2NF

每一个非主属性都完全函数依赖与R的码

可以采用投影法将一个1NF的关系分解为多个2NF的关系，这样可以一定程度上减轻1NF关系中存在的问题。但是并不能完全消除各种异常和冗余。

3NF

每一个非主属性不传递函数依赖与候选码

采用投影法将一个2NF关系分解为多个3NF关系，可以一定程度解决2NF存在的问题。但是不能完全消除。

不存在传递依赖

BCNF

每个属性都不部分依赖与候选码也不传递依赖于候选码。

2NF、3NF

性质：

所有非主属性都完全函数依赖与每个候选码
所有主属性都完全函数依赖与每个不包含它的候选码
没有任何属性完全函数依赖与非码的任何一组属性
在函数依赖范畴内，BCNF为最高范式
任何一个二目关系都是BCNF

如果关系R是BCNF，则R一定是3NF

如果R是3NF，而且R只有一个候选码，则R一定属于BCNF

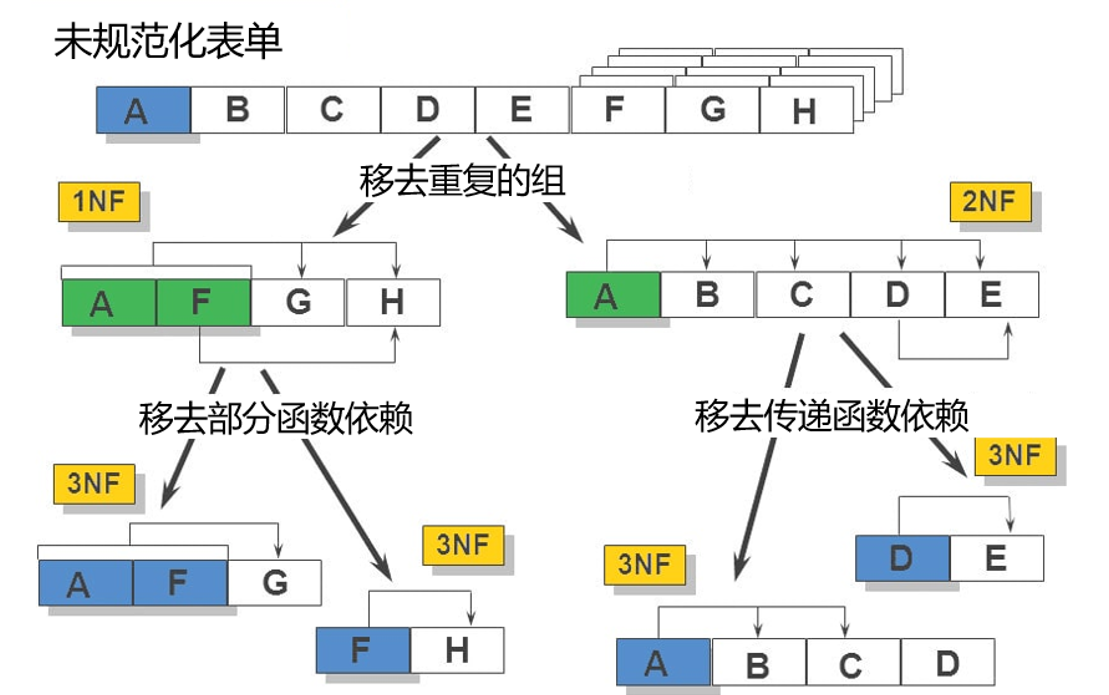
规范化过程

总结

853012-20181109110730391-1699550272

规范化的本质就是要提高数据的独立性，解决增删改异常和数据冗余的问题。用规范化的思想来解决数据依赖中不合适的部分。

1NF的目标：确保每列的原子性（不可分）
2NF的目标：确保每列都和候选键相关（完全依赖）
3NF的目标：确保每列都和候选键列直接相关，而不是间接相关（无传递依赖）

但是并不一定非要满足范式要求，有时候违背一下的设计反而更好。这种好是对于数据查询来讲要好。

每一次规范化都是减少插入异常、删除异常、冗余度大、修改复杂等问题

快速求候选码

属性划分：

–L类：仅出现在F的函数依赖左部的属性。

–R类：仅出现在F的函数依赖右部的属性。

–N类：在F的函数依赖左部和右部均未出现的属性。

–LR类：在F的函数依赖左部和右部两部均出现的属性。

定理：

定理1：若X(X∈R)是L类属性，则X必为R的任一候选码的成员。
- 推论1：若X(X∈R)是L类属性，且X+（X的闭包）包含了R的全部属性，则X必为R的唯一候选码。
定理2：若X(X∈R)是R类属性，则X不在任何候选码中。
定理3：如果X是R的N类属性，则X必包含在R的任一候选码中。
- 推论2：如果X是R的N类和L类组成的属性集，且X+（X+的闭包）包含了R的所有属性，则X是R的唯一候选码。

其实画图最快

第6章

1.理解并给出函数依赖、传递依赖的定义

答:设R(U)是属性集U上的关系模式。X，Y是属性集U的子集。若对于R(U)的任意一个可能的关系r，r中不可能存在两个元组在X上的属性值相等，而在Y上的属性值不等，则称X函数确定Y或Y函数依赖于X，记作XàY。（即只要X上的属性值相等，Y上的值一定相等。）

在R(U)中，如果X→Y，(Y Í X) ,Y→X Y→Z，则称Z对X传递函数依赖。

2.理解并给出部分函数依赖、完全函数依赖的定义

答: 在R(U)中，如果 XàY，并且对于X的任何一个真子集X’，都有X’ à Y，则称Y对X完全函数依赖

若XàY，但Y不完全函数依赖于X，则称Y对X部分函数依赖

3.理解并给出1 NF 、ZNF 、3NF 、BNF的定义

答:若关系模式R的每一个分量是不可再分的数据项，则关系模式R属于第一范式(1NF)。

若关系模式R∈1NF，且每一个非主属性完全函数依赖于码，则关系模式R∈2NF 。（即1NF消除了非主属性对码的部分函数依赖则成为2NF）。

若关系模式R∈2NF，且关系模式R中的所有非主属性对任何候选关键字都不存在传递信赖，则称关系R是属于第三范式的，则称R<U，R∈3NF。

关系模式R<U，F>∈1NF 。若XàY且Y不是X的子集时,X必含有码，则R<U，F>∈BCNF。

4.给出分解为3NF并保持依赖和无损分解的算法

答:（1）F的最小覆盖仍记为F，找出不在F中出现的R中属性，组成一个关系模式，将其从R中分离，其余属性仍组成的关系模式仍记为R，属性集记为U

（2）若最小覆盖F中有一函数依赖含有R中的所有属性，则把整个R作为输出，算法结束，否则进入（3）

（3）对于F中所有函数依赖X ®A，将XA作为s中的一个关系模式输出，但如果F中有函数依赖X ®A1，X ®A2，…，X ®An，可将XA1…An作为一个关系模式输出

（4）设X为R的一个键，则加上 {R（X）}，消除重复。

第六章关系数据理论