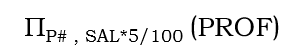第2章 关系代数
了解笛卡尔积,应该都会。
关系的性质:
- 每一列的数据必须来自同一个域
- 每一列必须是不可再分的数据项不能有相同的行
- 行列次序无关
关系模式
\[R(属性U,域D,映射关系dom,依赖关系F)\]三类关系表:
- 基本关系表:实际存在的表
- 查询表:查询结果对应的表
- 视图表,由基本表或者其他视图表导出来的表,一般不存储实际数据
**关系代数基本操作:**选择、投影、并、差、笛卡尔积,此外还有连接、除、交。
完整性约束
- 实体完整性(行):如果属性A是关系R的主属性,则属性A不能取空值。
- 引用完整性(表间):如果关系引用了一个关系的主码,则引用的这一列中的值必须是被引用列里面有的记录。
外码:假设F是基本关系R的一个或者一组属性,但不是R的码,如果F和基本关系S的主码Ks对应,则F是基本关系R的外码。此时称R为参照关系,S为被参照关系。
- 域完整性(列):针对某一个具体的关系数据库的约束条件,数据必须满足某一些语义要求。
关系代数
关系代数运算符:
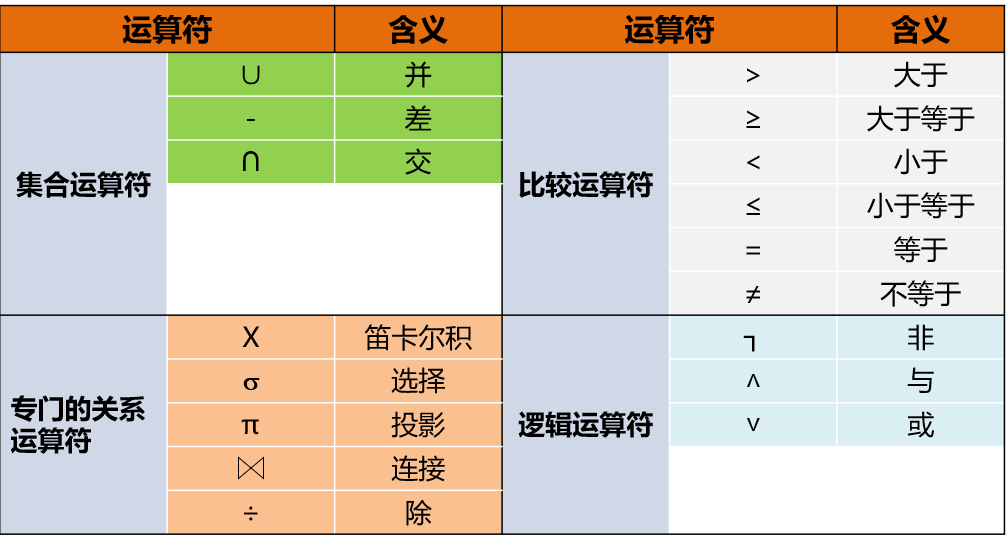
集合运算
- 并
- 差
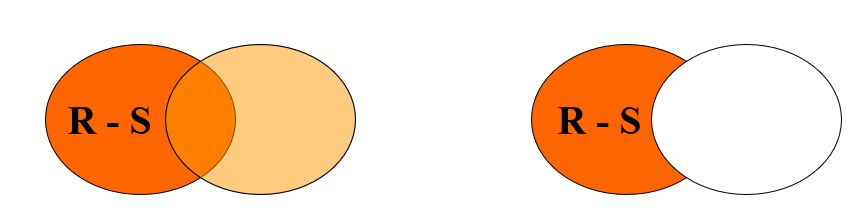
- 交
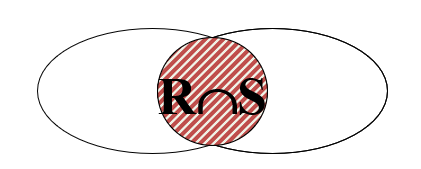
并的两个东东必须同类型,属性个数相同,次序相同。每一个元组在结果中只出现一次。
也就是相同的关系模式
- 笛卡尔积
表示的是两个关系对应元组集合之间可能的组合关系,是两个关系的无条件连接。
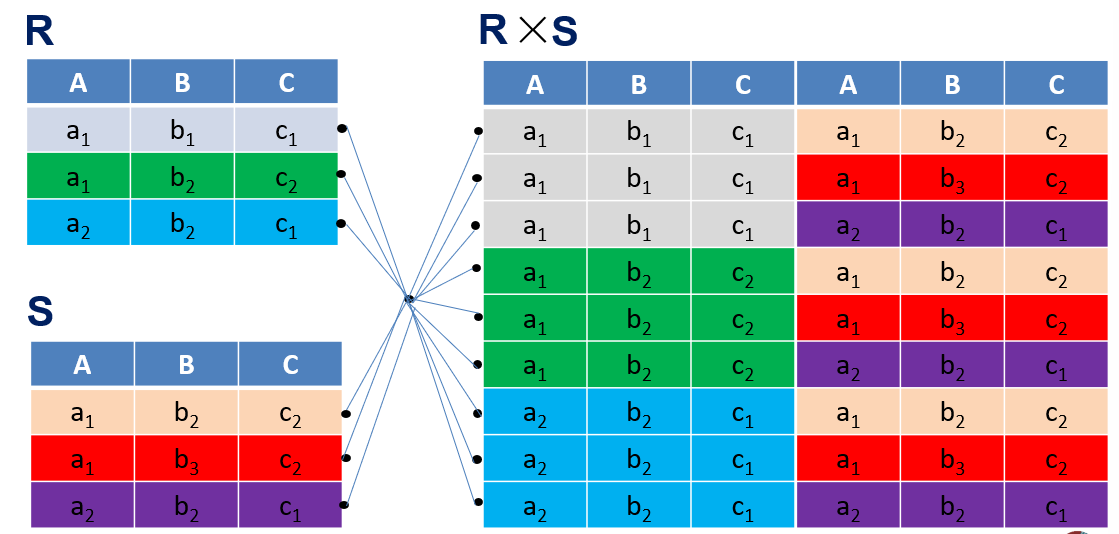
关系运算
https://blog.csdn.net/weixin_43222324/article/details/108485648
-
选择运算$\sigma$:
从关系R中选择满足给定条件为真的元组(从行的角度) \(\sigma_F(R) = {t | t ∈ R,F(t) = true}\)
σ选择,右下角F选择函数,括号R关系模式(表)
相当于dql中where和having
举例:

- 投影运算$\pi$:
从关系R中取出若干列组成新的关系(从列的角度) \(\Pi_A(R) = { t[A] | t∈R},t \subseteq R\)
Π投影选择列,右下角A选择的列,括号R关系模式(表)
相当于dql中select后的
举例:
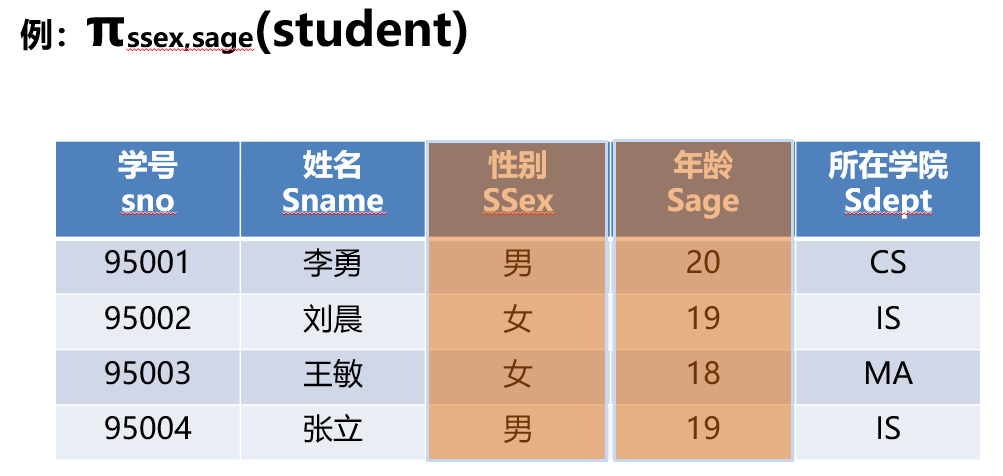
可以定义广义投影,就是投影的项目可以是算术表达式。
-
改名$\rho$:
显示改关系和属性名

ρ改名字,右下角S改后的名字,括号改之前的关系模式名
- 笛卡尔积
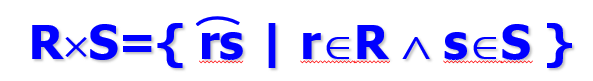
关系R和关系S笛卡尔积
- 内连接
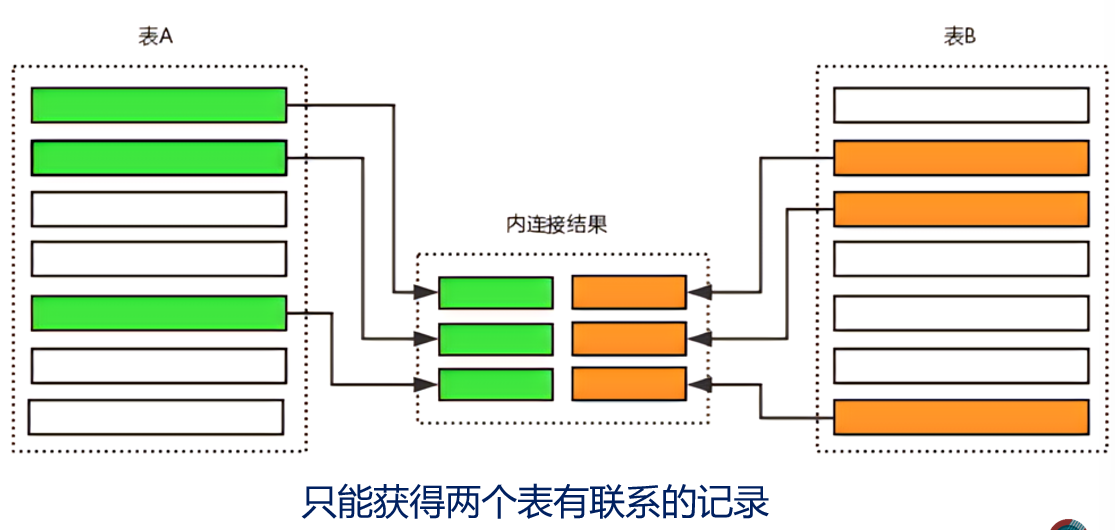
- $\theta$连接

θ运算符,A和B可比的属性列
举例:求数学成绩比王红同学高的学生
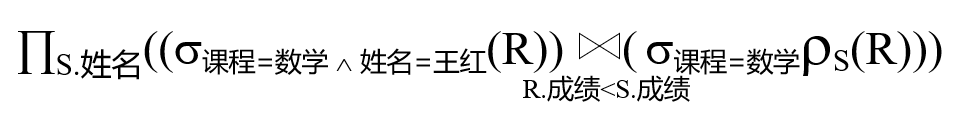
当$\theta$为等号的时候是等值连接
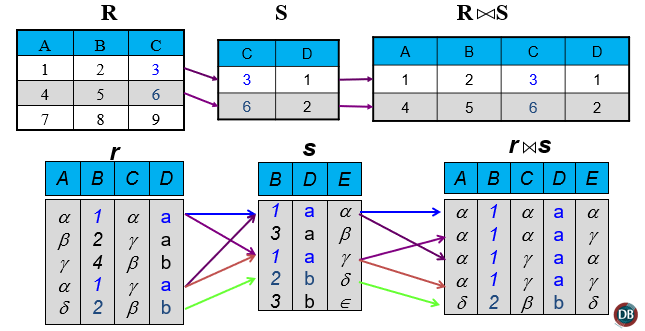
- 自然连接

自然连接中相等的分量必须是相同的属性组,并且要在结果中去除重复的属性,但是 等值连接就不会去除。
- 外连接
保留一个表的所有数据,另一个无关联的记录为null。外连接的主要目的是为了防止因为失配产生的信息丢失。

哪边外连接,那边的信息就会全部被保留。
赋值运算
就是可以用临时的关系变量 来保存阶段性的关系运算结果。通过赋值给临时关系变量进行结果的传递。 \(临时关系变量 \longleftarrow 关系代数表达式\)
注意:给永久关系的复制意味着对数据库的修改。
聚集函数
求一组值的统计信息,返回单一的值。


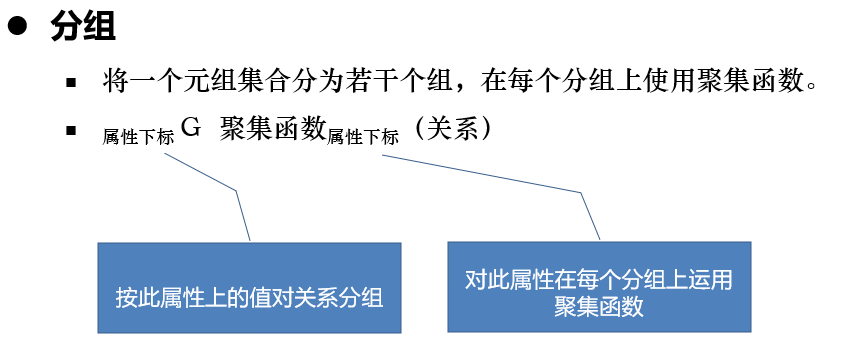
举例:

G分组函数,左下角分组的对象相当于group by,右下角表示使用的聚合函数,相当于select,括号为关系模式(表)
第2章 关系数据库
\1. 试述关系模型的完整性规则。
答:关系模型的完整性规则有实体完整性规、参照完整性规则和用户定义完整性规则。
实体完整性规则是指若属性A是基本关系R的主码属性,则属性A不能取空值。
参照完整性规则是指若属性(或属性组)F是基本关系R的外码,它与基本关系S的主码Ks相对应(基本关系R和S不一定是不同的关系),则对于R中每个元组在F上的值必须为:或者取空值(F的每个属性值均为空值);或者等于S中某个元组的主码值。
用户定义的完整性是针对某一具体关系数据库的约束条件。它反映某一具体应用所涉及的数据必须满足的语义要求。包括某属性取唯一值,某一属性值应满足一定的函数关系,某一属性的取值范围等等。
\2. 在参照完整性中,为什么外部码属性的值也可以为空?什么情况下才可以为空?
答:外部码属性不一定是(自身关系模式)主码属性,所以外部码属性的值可能为空。当外部码属性不是主码属性时,可以取空值,否则不能取空值。
3.试述关系模型的三个组成部分。 答:关系模型由关系数据结构、关系操作集合和关系完整性约束三部分组成。
4.解释候选码和主码的关系。
答:
若关系中的某一属性组的值能唯一标识一个元组,而其子集不能,该属性组称为候选码;如果一个关系有多个候选码,可以选择其中一个为主码。候选码可以有多个,主码是其中的一个。